Study note:激发态的波函数分析方法
记录下使用Gaussian与Multiwfn如何做激发态分析。
注意:理论部分内容是一位初学者的思考,未必完全正确,会随笔者学习理解过程随时更新。如果读者发现任何地方与已有认识不符,不要怀疑,一定是笔者理解有误,请务必在评论区指出!
目录
- 1. 前线轨道(Frontier Molecular Orbitals, FMOs)
- 2. 跃迁密度(Transition Density)
- 3. 跃迁偶极矩密度(Transition Dipole Moment Density)
- 4. 跃迁偶极矩(Transition Dipole Moment, TDM)
- 5. 自然跃迁轨道(Natural Transition Orbital, NTO)
- 6. 空穴-电子分析(Hole-Electron Analysis)
- 7. 密度差 (Density Difference)
- 8. 定量电荷转移分析
1. 前线轨道(Frontier Molecular Orbitals, FMOs)
由于荧光通常感兴趣的激发态都是较低的价层激发,前线轨道常常是激发的主要参与者。我们可以利用Gaussian布居分析和TD-HF/TD-DFT计算打印的组态系数来检查参与激发的轨道,从而推断电子的流向。以乙烯为例,我们首先需要进行结构优化:
1
2
3
%chk=ethene.chk
# opt freq HF/def2TZVP
...
由于我们接下来会反复使用分子轨道的概念,这里就使用HF进行演示,避免杂化泛函影响轨道图像;而在实际研究时,读者仍然应当根据体系选择合适的泛函,绝对不要照抄本文的TD-HF演示。
优化结构后,进行TD-HF/TD-DFT计算:
1
2
%chk=ethene.chk
# td HF/def2TZVP
log文件中会打印组态系数:
1
2
3
4
5
Excited State 1: Singlet-BU 7.7662 eV 159.65 nm f=0.4369 <S**2>=0.000
8 -> 9 0.69503
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -77.7801148629
Copying the excited state density for this state as the 1-particle RhoCI density.
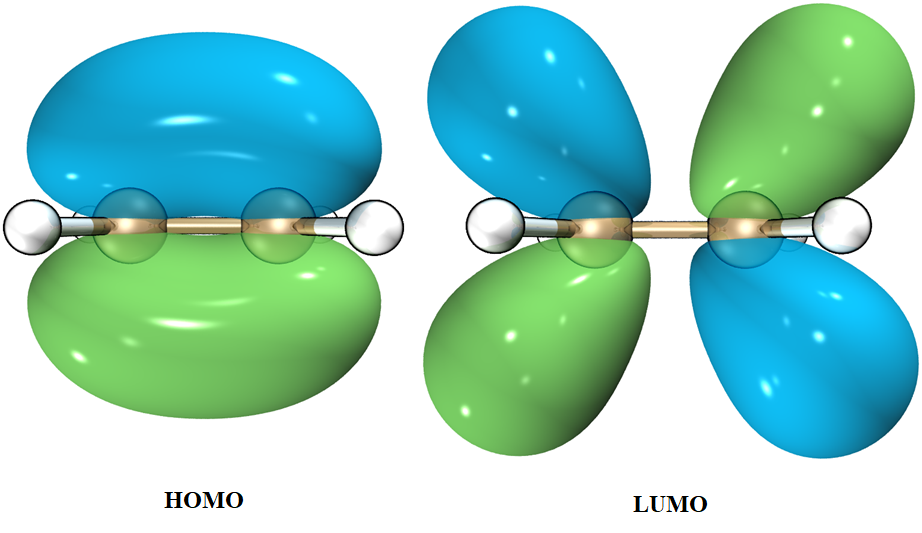
我们看到,乙烯的第一激发态由MO8 → MO9主导,组态系数0.69503,因此MO8 → MO9跃迁对S1的贡献大约是96.6%,我们可以通过MO8、9的形状来了解这个激发是什么性质。使用Multiwfn导出分子轨道:
1
2
3
4
5
6
7
8
ethene.fchk
200
3 // 导出分子轨道
h // HOMO
1 // 小分子,低质量格点就够
3
l // LUMO
1
HOMO是乙烯的$π$成键轨道;LUMO是乙烯的$π$反键轨道。由此,我们可以知道乙烯的S1激发时,双键会被削弱,此时中央C-C键应当可以自由旋转。
2. 跃迁密度(Transition Density)
一个比较简单的抽象概念。如果假设激发态可以用单对MO跃迁来描述,则跃迁密度可以表示为:
\[\rho_{ij}(r) = \psi_{i}^*(r)\psi_{j}(r)\]跃迁密度描述的是在空间位置r处态i与态j电子与空穴的重叠。为了让Multiwfn绘制出跃迁密度等值面,我们进行TD-HF/TD-DFT计算同上,然后取fchk与log文件,使用Multiwfn分析
1
2
3
4
5
6
7
8
ethene.fchk
18
1
ethene.log // 载入log
1 // 分析第一激发态
1 // 可视化
1
5 // 绘制跃迁密度等值面
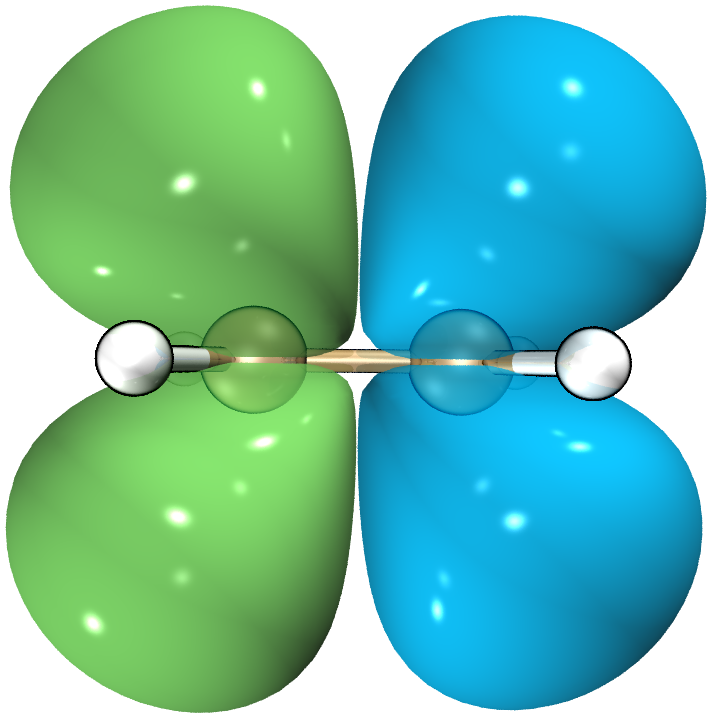
最终效果:
我们看到,跃迁密度只出现在激发过程涉及的位置。跃迁密度全空间积分为0,体现了跃迁过程中总体电子守恒。
Ref:
3. 跃迁偶极矩密度(Transition Dipole Moment Density)
跃迁密度展示了偶极的雏形。回忆偶极矩的计算方法$ \mu = -e \times \boldsymbol{r} $,要描述跃迁偶极,我们还需要引入位置和电荷两个量。这里我们首先对跃迁密度引入位置矢量$\boldsymbol{r}$,得到跃迁偶极矩密度:
\[\boldsymbol{\rho}_{ij}^{dip(\boldsymbol{r})}(r) = \psi_{i}^*(r) {\boldsymbol{r}} \psi_{j}(r)\]跃迁偶极矩密度反映了体系位置$\boldsymbol{r}$处对跃迁偶极矩的贡献。绘制跃迁偶极矩密度等值面时,Gaussian计算与前述一致。使用Multiwfn分析:
1
2
3
4
5
6
7
8
9
ethene.fchk
18
1
ethene.log
1
1
1 // 到此处为止操作不变
6 // 绘制跃迁偶极矩等值面
{1,2,3,4} // 根据需求选择绘制的分量
为了在三维空间展示出跃迁偶极矩密度等值面,我们每次只能绘制一个分量。假设乙烯双键的方向为X,垂直于双键方向为Y,垂直于乙烯平面的方向为Z,三个分量跃迁偶极矩密度等值面图形如下: 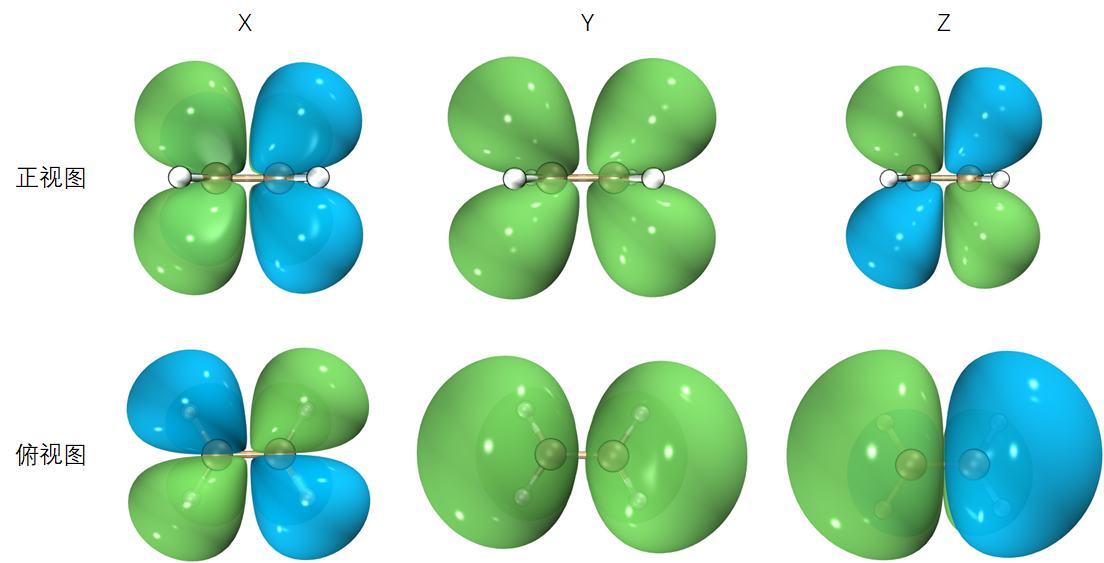
可见,由于引入了位置矢量,跃迁偶极矩密度相较于跃迁密度发生了部分变号,同时对称性也发生了改变,其造成的影响将在下一节讨论。跃迁偶极矩密度可以单独考察XYZ三个分量跃迁偶极矩贡献分布情况,实际用的比较少。
4. 跃迁偶极矩(Transition Dipole Moment, TDM)
对跃迁偶极矩密度积分,并引入电荷,得到跃迁电偶极矩$\mu_{ij}^e$:
\[\boldsymbol{\mu}_{ij}^e = -e \int \boldsymbol{\rho}_{ij}^{dip}(\boldsymbol{r}) d^3r\]或者定义跃迁电偶极算符:
\[\hat{\boldsymbol{\mu}^e} = −e \hat{\boldsymbol{r}}\]则TDM表达式为:
\[\boldsymbol{\mu}_{ij}^e = \langle \psi_i|\hat{\boldsymbol{\mu}^e}|\psi_j \rangle\]$\mu_{ij}^e$反映了分子吸收电磁辐射的能力,只有当$\mu_{ij}^e ≠ 0$时,跃迁才是电偶极允许的。若$\mu_{ij}^e = 0$,跃迁电偶极禁阻,意味着跃迁很难(也许能通过磁偶极跃迁、电四极跃迁等)发生或根本不发生。
注意到计算TDM时对跃迁偶极矩密度进行了积分。因此,当跃迁偶极矩密度等值面呈现奇对称时,积分结果为0,则跃迁将是严格禁阻的,而呈非对称与偶对称的跃迁偶极矩密度则无此行为;
由于跃迁偶极矩密度来自于跃迁密度,进一步反推可知当跃迁密度关于X=0偶对称时,由于$\boldsymbol{x}$是奇对称的,最终被积函数为奇×偶=奇函数,积分得到的X分量跃迁偶极矩将为0,对Y、Z分量同理,而呈非对称与奇对称的跃迁密度则无此行为;
跃迁密度被定义为两个电子态波函数的积,可知两个电子态波函数的对称性可能最终影响跃迁是否能发生,这是对称性选择定则的来源。
TDM本身的计算只需要Gaussian进行TD-HF/TD-DFT计算即可,在输出文件中将直接打印:
1
2
3
4
5
Ground to excited state transition electric dipole moments (Au):
state X Y Z Dip. S. Osc.
1 0.0000 -1.5153 0.0000 2.2960 0.4369
2 0.0000 0.0000 0.3430 0.1176 0.0255
3 0.0000 0.0000 0.0000 0.0000 0.0000
可见S1只有Y分量的有非零TDM,与前面看到Y分量的跃迁偶极矩密度偶对称相符。
利用Gaussian输出文件,可以使用Multiwfn绘制矩阵热图。因为乙烯就俩重原子,画出来没啥意义,此处以及后续电荷转移分析的部分展示的都是笔者做的其他体系:
1
2
3
4
5
6
7
8
9
10
11
othersys.fchk
18
2 // 绘制原子/片段跃迁矩阵的热图
othersys.log
1
n
1 // 收缩模式1
-1 // 定义片段
0 // 读入外部文件
frag.txt
2 // 也可以用选项1来观看,5来改色彩刻度
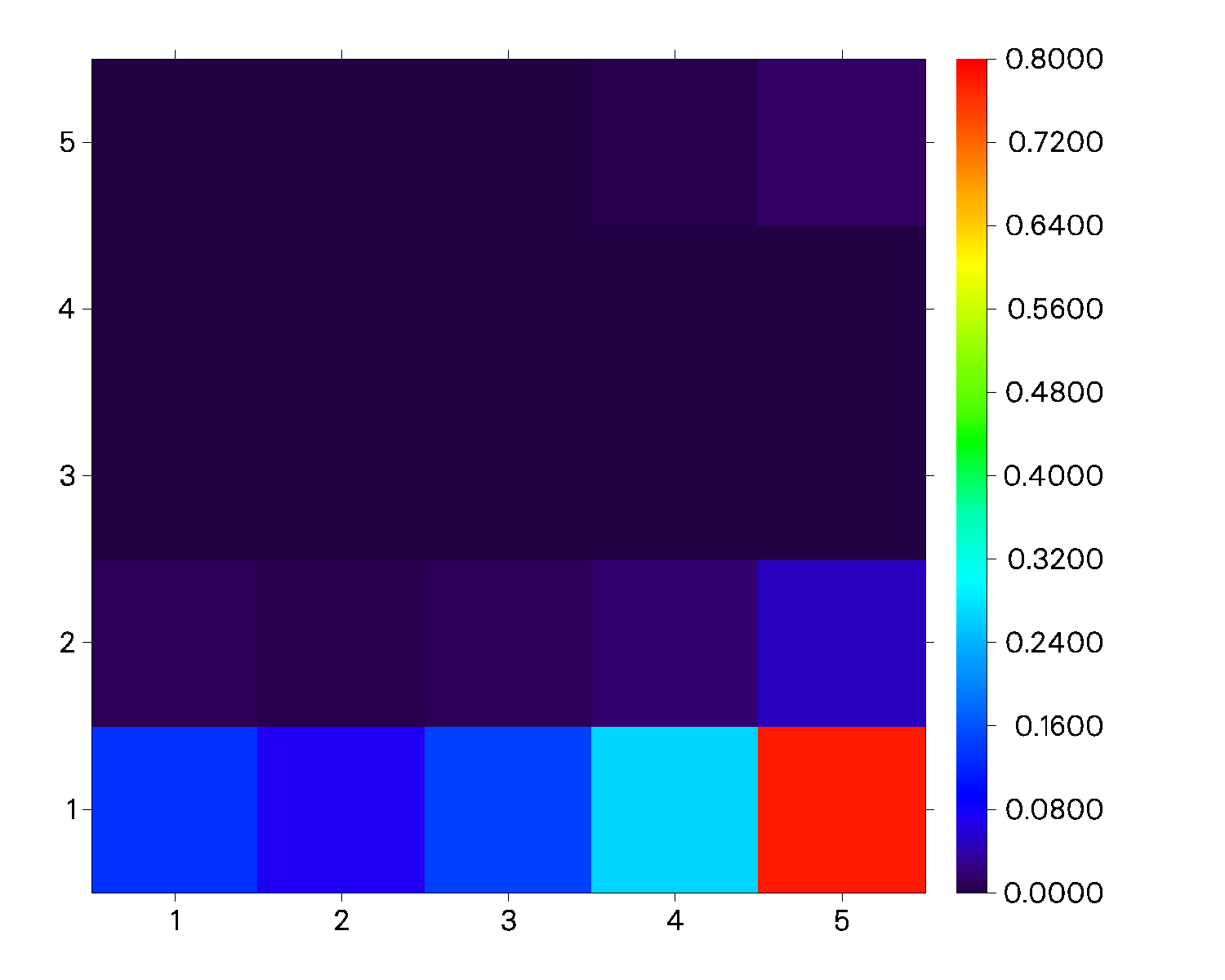
此时当前目录下保存了刚刚绘制的热图:
图片横坐标对应空穴位置,纵坐标对应电子位置。从图中可以看到空穴主要出现在片段5,其余片段只有少部分分布;而电子则几乎只分布在片段1处,由此我们可以推测此处主要是片段5向片段1转移了电子。
5. 自然跃迁轨道(Natural Transition Orbital, NTO)
在TD-HF/TD-DFT计算中,激发态通常是多个基态MO对的线性组合(此处将激发和去激发简写在一起了):
\[|\Psi_{\text{exc}}\rangle = \sum_{ia} w_{ia} \hat{a}^\dagger_a \hat{a}_i |\Psi_0\rangle\]式中:
- $i$: 占据轨道
- $a$: 虚轨道
- $w_{ia}$: 组态系数
- $\hat{a}^\dagger_a \hat{a}_i$: 表示从轨道 $i$ 激发到 $a$
这里的MO是从基态自洽场计算得到的,适合描述基态电子分布,却不一定最适合描述激发态的电子跃迁。因此在一些情况下,电子激发是没有主导的MO对的:
1
2
3
4
5
6
7
8
Excitation energies and oscillator strengths:
Excited State 1: Singlet-A 2.1855 eV 567.31 nm f=1.4596 <S**2>=0.000
209 -> 211 0.50093
210 -> 211 -0.46903
This state for optimization and/or second-order correction.
Total Energy, E(TD-HF/TD-DFT) = -2799.53472176
Copying the excited state density for this state as the 1-particle RhoCI density.
此时,基于MO进行分析并不直观。为了解决这个问题,首先定义跃迁密度矩阵:
\[T_{ia} = w_{ia}\]它记录了从每个占据轨道激发到每个虚轨道的权重。随后,进行奇异值分解:
\[T = U \, \Lambda \, V^\dagger\]式中:
- $U$:可以将正则占据轨道变换为占据NTO的神奇妙妙酉矩阵
- $V$:可以将正则虚轨道变换为虚NTO的神奇妙妙酉矩阵
- $\Lambda$:对角矩阵,包含奇异值,描述了跃迁的强度
奇异值分解的目的是找到一个投影方向,使得激发态可以尽可能由一对轨道描述:
\[|\Psi_{\text{exc}}\rangle \approx \lambda \, |\phi^{\text{occ}}_{NTO} \rightarrow \phi^{\text{vir}}_{NTO}\rangle\]NTO的产生方式见从量子化学软件中产生波函数。以Gaussian输出为例,使用pop=(NTO,saveNTO)进行计算后,原本是占据数的地方写入的是NTO对的本征值,乘以100%就是该NTO对占激发的百分比。
1
2
3
4
5
6
Alpha occ. eigenvalues -- 0.00018 0.00021 0.00022 0.00022 0.00026
Alpha occ. eigenvalues -- 0.00027 0.00027 0.00028 0.00029 0.00035
Alpha occ. eigenvalues -- 0.00049 0.00092 0.00293 0.01679 0.97920
Alpha virt. eigenvalues -- 0.97920 0.01679 0.00293 0.00092 0.00049
Alpha virt. eigenvalues -- 0.00035 0.00029 0.00028 0.00027 0.00027
Alpha virt. eigenvalues -- 0.00026 0.00022 0.00022 0.00021 0.00018
可以看到,原本必须要两个轨道对才能描述的跃迁现在可以通过单对NTO轨道来描述(HONTO→LUNTO=97.92%),如此讨论时就方便多了。
另外,NTO本身也是一种自然轨道,可以进行各种轨道分析,例如此贴中第三节展示的通过考察轨道成份计算电荷转移百分比。
Ref:
6. 空穴-电子分析(Hole-Electron Analysis)
有时候,对跃迁密度矩阵进行SVD分解也不能构造出一对主导的轨道,此时进行酉变换的价值大大削减了。在讨论这类体系时,可以使用空穴-电子分析。空穴-电子分析是一种相较于NTO更激进的约化方法,思想是舍弃掉波函数相位信息,单独构造一对”轨道”将所有轨道跃迁纳入考虑,使得电子与空穴均可以通过这对”轨道”进行描述。在不需要相位相关信息时,空穴-电子分析可以完全代替NTO作为一种普适的激发态分析手段。
空穴-电子分析在Multiwfn中实现是基于TD-DFT/CIS的,总空穴密度被定义为:
\[\rho^{\text{hole}}(\mathbf{r}) = \rho^{\text{hole}}_{\text{loc}}(\mathbf{r}) + \rho^{\text{hole}}_{\text{cross}}(\mathbf{r})\]其中,局域空穴密度是组态函数自身的贡献,定义为:
\[\rho^{\text{hole}}_{\text{loc}}(\mathbf{r}) = \sum_{i \to a} (w_i^a)^2 \varphi_i \varphi_i - \sum_{i \leftarrow a} (w_i'^{a})^2 \varphi_i \varphi_i\]式中:
- $w_i^a$:从占据轨道 $i$ 到虚轨道 $a$ 的激发组态系数
- $\varphi_i$:占据轨道
- $(w_i^a)^2$、$(w_i’^a)^2$:激发组态的权重
- $i \to a$:表示激发贡献
- $i \leftarrow a$:表示去激发贡献
交叉空穴密度体现组态函数之间的耦合对空穴和电子分布的影响,定义为:
\[\rho^{\text{hole}}_{\text{cross}}(\mathbf{r}) = \sum_{i \to a} \sum_{j \neq i \to a} w_i^a w_j^a \varphi_i \varphi_j - \sum_{i \leftarrow a} \sum_{j \neq i \leftarrow a} w_i'^{a} w_j'^a \varphi_i \varphi_j\]式中:
- $i \neq j$:不同的占据轨道
- $w_i^a w_j^a$:不同激发组态间的交叉权重
- $\varphi_i \varphi_j$:不同轨道间的交叉项
电子项形式跟空穴类似:
\[\rho^{\text{ele}}(\mathbf{r}) = \rho^{\text{ele}}_{\text{loc}}(\mathbf{r}) + \rho^{\text{ele}}_{\text{cross}}(\mathbf{r})\] \[\rho^{\text{ele}}_{\text{loc}}(\mathbf{r}) = \sum_{i \to a} (w_i^a)^2 \varphi_a \varphi_a - \sum_{i \leftarrow a} (w_i'^{a})^2 \varphi_a \varphi_a\] \[\rho^{\text{ele}}_{\text{cross}}(\mathbf{r}) = \sum_{i \to a} \sum_{i \to b \neq a} w_i^a w_i^b \varphi_a \varphi_b - \sum_{i \leftarrow a} \sum_{i \leftarrow b \neq a} w_i'^{a} w_i'^{b} \varphi_a \varphi_b\]进行空穴-电子分析需要进行TD-HF/TD-DFT计算。由于要在Multiwfn中根据组态系数构造激发态非弛豫密度,在计算时需要使用至少IOp(9/40=3)来打印更多组态系数:
1
# opt freq HF/def2TZVP IOp(9/40=3)
然后使用Multiwfn进行分析:
1
2
3
4
5
6
7
8
ethene.fchk
18
1
ethene.log
1
1
1 // 到此为止与跃迁密度等值面一致
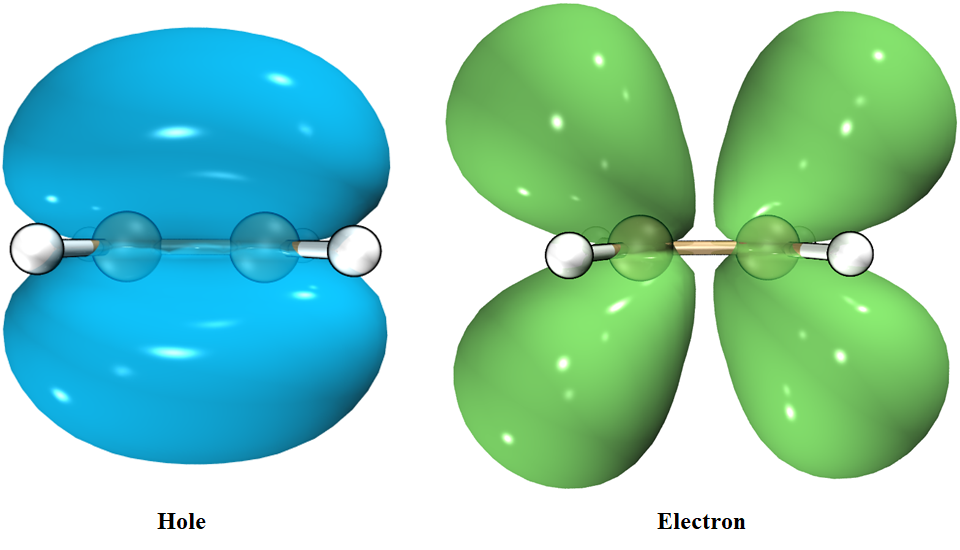
{1,2,3} // 可视化电子-空穴
我们看到空穴形状像乙烯的$π$成键轨道,而电子像$π$反键轨道,与MO的结果是一致的。
电子空穴分析还支持使用高斯函数将空穴和电子分布平滑化描述,在图形上展示的更清楚,这里就不放图了
Ref: 使用Multiwfn做空穴-电子分析全面考察电子激发特征
7. 密度差 (Density Difference)
TD-DFT/TD-HF计算用的是线性响应理论,不能直接得到激发态的波函数,但是可以利用跃迁密度矩阵来构造激发态密度。激发态密度有弛豫的与非弛豫的两种,区别见此贴的讨论。简单来讲,弛豫密度更接近真实激发态密度,但要花费更多的时间去计算;而非弛豫密度用基态轨道和组态系数就可以构造,物理意义可理解为在激发一瞬间电子尚未发生重排时的激发态密度,也可以认为是真实激发态密度的一阶近似。有了激发态密度,将之与基态密度做差就可以知道跃迁过程中哪些地方电子密度增加或减少。
7.1. 非弛豫密度差
非弛豫密度差有两种方式得到,一种是基于自然轨道做差,一种是基于空穴与电子密度做差。这两种方法得到的非弛豫密度差是等价的,不过基于log文件构造密度差可能因为组态系数的打印阈值而与基于完整CI矩阵构造的密度差产生一定差异。
先来看直接使用自然轨道做差的方式:
\[Δρ_e= \rho_{i} - \rho_{j}\]这样求得的密度差在sob老师的博文中被称作电子密度差(Electron Density Difference)。要计算电子密度差,首先需要在density下做一次TD-HF/TD-DFT计算:
1
# td HF/def2TZVP density
将本计算的fchk文件载入Multiwfn,导出基态与激发态自然轨道:
1
2
3
4
5
ethene_density.fchk
200
16
SCF // 载入基态密度
y // 输出到new.mwfn
此处暂停,手动把new.mwfn改名,避免接下来操作覆盖此文件,然后重新打开Multiwfn并继续:
1
2
3
4
5
ethene_density.fchk
200
16
CI Rho(1) // CI Rho(1)字段记录了未弛豫的密度矩阵
y // 输出到new.mwfn
随后重新打开Multiwfn,在主功能5中进行做差:
1
2
3
4
5
6
7
CI_Rho.mwfn // 激发态的自然轨道
5
0 // 设定自定义运算
1 // 只有1个文件要对已读入的波函数进行运算
-,SCF.mwfn // 运算符和文件名
1 // 电子密度函数
1 // 小分子,低等质量格点即可
电子密度差可以对任意两个态之间求得,不局限于基态与激发态,因此也可以用于计算激发态之间的假想激发。
Ref:
再来看基于基于空穴与电子定义的电荷密度差(Charge Density Difference, CDD):
\[Δρ_c(\mathbf{r})=ρ^{\text{ele}}(\mathbf{r})-ρ^{\text{hole}}(\mathbf{r})\]计算参考空穴-电子分析(Hole-Electron Analysis),Multiwfn同样是由主功能18处理:
1
2
3
4
5
6
7
8
ethene.fchk
18
1
ethene.log
1
1
1 // 到此为止与空穴-电子分析一致
7 // 作CDD图
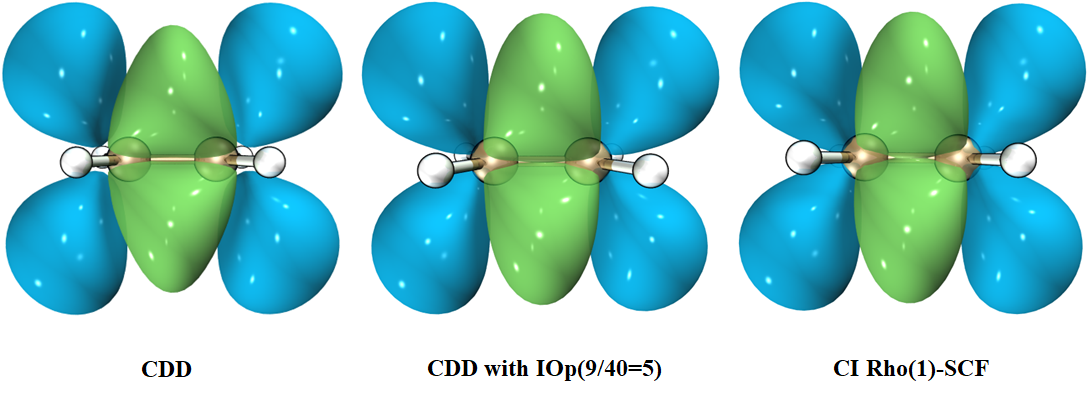
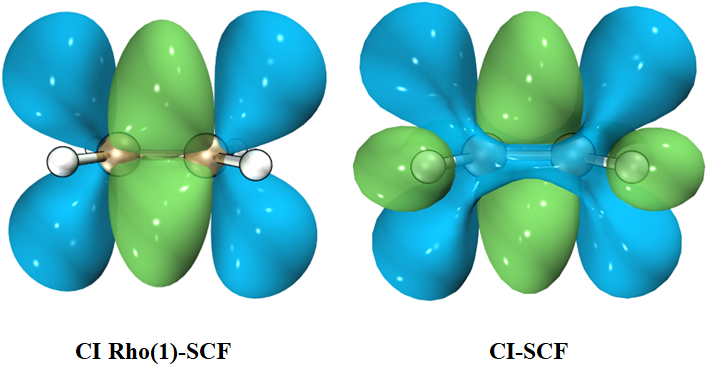
我们将电子密度差与电荷密度差放在一起对比:
可以看到,在使用IOp(9/40=5)修改打印阈值的情况下,电子密度差与电荷密度差基本一致;而若使用默认的打印阈值,最终做出的CDD等值面存在着肉眼可见的误差。
Ref: 使用Multiwfn做空穴-电子分析全面考察电子激发特征
7.2. 弛豫密度差
由于空穴-电子分析基于非弛豫密度,弛豫密度差应用自然轨道做差求得。其步骤与非弛豫密度差完全一致,但导出自然轨道时要读取CI字段保存的密度矩阵来构造弛豫密度:
1
2
3
4
5
ethene_density.fchk
200
16
CI // CI字段记录了弛豫的密度矩阵
y // 输出到new.mwfn
可以看到,非弛豫与弛豫密度展现出的性质还是存在一定差异的。尽管如此,由于弛豫密度计算耗时很久,且部分级别根本没有实现输出弛豫密度,实际使用时依然多采用非弛豫密度。
sob老师的观点是通常非弛豫密度虽然在原理上没有基于弛豫的激发态密度的那么严格,但是对于讨论电子激发特征是足够的。
8. 定量电荷转移分析
8.1. 片段原子电荷
我们可以基于激发前后原子电荷求差来判断片段间电荷转移情况。需要参考上一节带density进行一次计算,并导出基态与激发态的自然轨道,随后:
1
2
3
4
5
6
SCF.mwfn // 载入基态密度
7 // 布居分析与原子电荷计算
-1 // 定义片段
1-10 // 计算某片段的电荷
11 // ADCH电荷
1 // 对称化
此时程序给出了所有原子的电荷以及片段的ADCH电荷:
1
2
Fragment charge: -0.21305560
Fragment population: 23.21305560
如法炮制,计算激发态的片段电荷,得到:
1
2
Fragment charge: -0.03060325
Fragment population: 40.03060325
发现电荷减少了,因此激发过程中电子总体是从当前片段中转移出去了。可以如此法继续计算其他片段的电荷,通过片段电荷增减情况来推测电荷转移情况。
Ref: 电子激发过程中片段间电荷转移百分比的计算
8.2. 空穴-电子热图
根据空穴与电子的定义,我们还可以如下定义出MO对电子与空穴的贡献:
\[\Theta_i^{\text{hole}} = \sum_a [(w_i^a)^2 - (w_i'^{a})^2]\] \[\Theta_a^{\text{ele}} = \sum_i [(w_i^a)^2 - (w_i'^{a})^2]\]通过类Mulliken方式的划分,可以实现原子和基函数对空穴与电子的贡献,据此可以绘制空穴-电子热图。
同样地,乙烯太小了,这里用其他体系进行演示:
1
2
3
4
5
6
7
othersys.fchk
18
1
othersys.log
1 // 到此为止与上一致
3 // 绘制热图
1 // Mulliken
此时屏幕上会打印各原子对电子空穴的贡献:
1
2
3
4
5
6
7
Contribution of each non-hydrogen atom to hole and electron:
1(C ) Hole: 0.56 % Electron: 4.20 % Overlap: 1.53 % Diff.: 3.64 %
2(C ) Hole: 0.32 % Electron: 3.90 % Overlap: 1.11 % Diff.: 3.58 %
3(C ) Hole: 1.24 % Electron: 0.51 % Overlap: 0.79 % Diff.: -0.73 %
4(C ) Hole: 0.14 % Electron: 3.37 % Overlap: 0.69 % Diff.: 3.22 %
5(C ) Hole: 0.95 % Electron: 4.07 % Overlap: 1.97 % Diff.: 3.11 %
...
我们继续定义片段,来获得更清晰的划分:
1
2
3
-1 // 定义片段
0
frag.txt
此时,屏幕上会打印每个片段的电子与空穴占比。
1
2
3
4
5
6
Contribution of each fragment to hole and electron:
# 1 Hole: 8.49 % Electron: 95.39 % Overlap: 28.46 % Diff.: 86.90 %
# 2 Hole: 0.43 % Electron: 4.23 % Overlap: 1.35 % Diff.: 3.80 %
# 3 Hole: 4.22 % Electron: 0.27 % Overlap: 1.06 % Diff.: -3.96 %
# 4 Hole: 19.47 % Electron: 0.02 % Overlap: 0.70 % Diff.: -19.45 %
# 5 Hole: 67.39 % Electron: 0.09 % Overlap: 2.42 % Diff.: -67.30 %
我们看到空穴集中在片段1,而空穴在片段4与5上分布较多。为了更好地可视化,使用选项1显示如下图形: 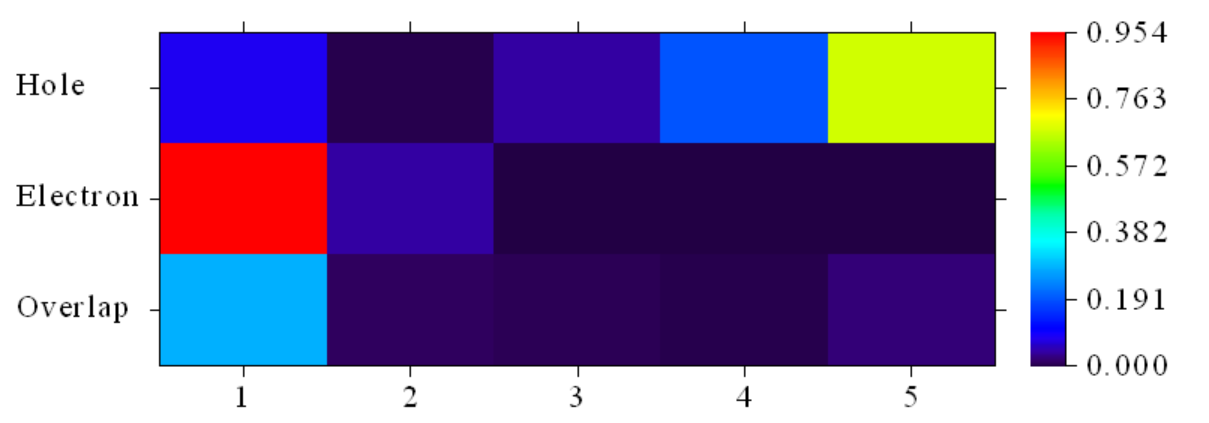
可以看到与数值对应的较好。该激发产生了片段5向片段1的电荷转移,与跃迁偶极矩矩阵图给出了相同的结论;但从此图中,我们还能看到此激发态混合了小部分片段1的局域激发。
Ref: 使用Multiwfn做空穴-电子分析全面考察电子激发特征
8.3. 片段电荷转移分析(Interfragment Charge Transfer Analysis, IFCT)
IFCT仍然使用前述Multiwfn空穴-电子分析定义的量,且也是基于片段对空穴和电子的贡献实现的。定义R→S的电子转移量$Q_{R,S}$:
\[Q_{R,S} = \Theta_{R,\text{hole}} \Theta_{S,\text{ele}}\]式中:
- $\Theta_{R,\text{hole}}$:体现了被激发的电子中来自片段R的有多少
- $\Theta_{S,\text{ele}}$:体现了电子要去的地方片段S贡献多少
可知当R占空穴越多,S占电子越多,则R→S转移的电子就越多,于是可以求得片段间净电子转移量:
\[p_{S→R} = Q_{S,R} - Q_{R,S}\]还可以求得某片段的电子净变化量:
\[\Delta p_R = \sum_{S≠R} p_{S→R} = \sum_{S≠R} (Q_{S,R} - Q_{R,S})\]计算参考空穴-电子分析(Hole-Electron Analysis),使用Multiwfn主功能18的模块8进行IFCT分析:
1
2
3
4
5
6
7
8
othersys.fchk
18
8
othersys.log
1
1 // 第一激发态
0
frag.txt
此时,程序会分析出每个片段间的电荷转移情况,并计算此激发态的电荷转移激发、局域激发成分:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Contribution of each fragment to hole and electron:
1 Hole: 8.49 % Electron: 95.39 %
2 Hole: 0.43 % Electron: 4.23 %
3 Hole: 4.22 % Electron: 0.27 %
4 Hole: 19.47 % Electron: 0.02 %
5 Hole: 67.39 % Electron: 0.09 %
Construction of interfragment charger-transfer matrix has finished!
...
Transferred electrons between fragments:
1 -> 2: 0.00359 1 <- 2: 0.00410 Net 1 -> 2: -0.00051
1 -> 3: 0.00023 1 <- 3: 0.04028 Net 1 -> 3: -0.04005
1 -> 4: 0.00002 1 <- 4: 0.18574 Net 1 -> 4: -0.18572
1 -> 5: 0.00007 1 <- 5: 0.64282 Net 1 -> 5: -0.64275
2 -> 3: 0.00001 2 <- 3: 0.00179 Net 2 -> 3: -0.00177
2 -> 4: 0.00000 2 <- 4: 0.00824 Net 2 -> 4: -0.00824
2 -> 5: 0.00000 2 <- 5: 0.02851 Net 2 -> 5: -0.02850
3 -> 4: 0.00001 3 <- 4: 0.00052 Net 3 -> 4: -0.00051
3 -> 5: 0.00004 3 <- 5: 0.00180 Net 3 -> 5: -0.00176
4 -> 5: 0.00017 4 <- 5: 0.00017 Net 4 -> 5: 0.00000
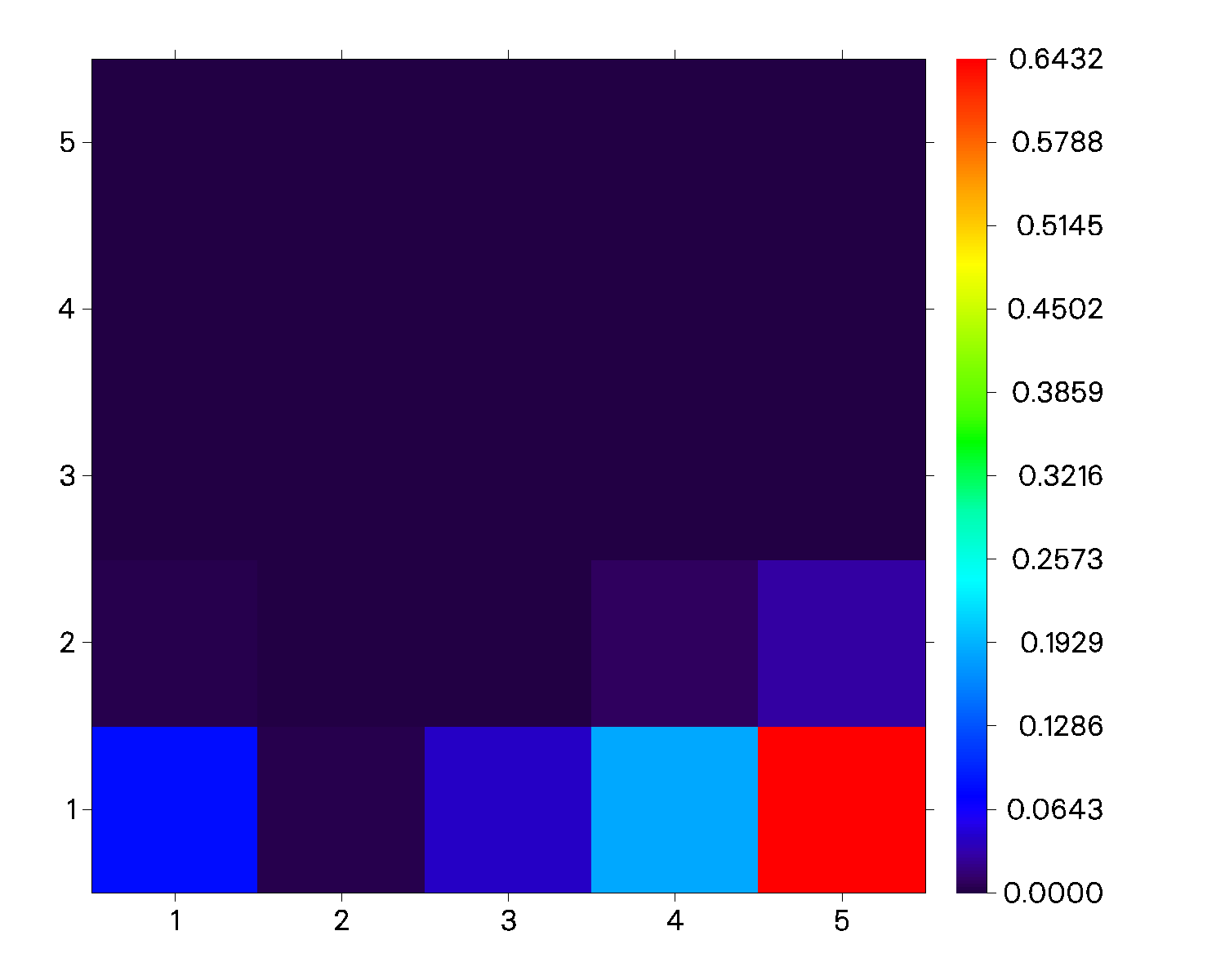
Intrinsic charge transfer percentage, CT(%): 91.810 %
Intrinsic local excitation percentage, LE(%): 8.190 %
我们看到,片段5向片段1转移电子量达到了0.64282,CT%成分91%,是个比较典型的CT激发。相较于片段原子电荷,IFCT的好处是可以定义任意多的片段,同时与空穴-电子分析的结果严格对应。另外,我们也可以根据IFCT的结果绘制电荷转移矩阵:
1
2
3
4
5
6
7
othersys.fchk
18
8
1
othersys.log
1 // 第一激发态
-1 // 导出原子-原子电荷转移矩阵
此时生成了atmCTmat.txt文件。
1
2
3
4
5
6
2 // 绘制矩阵填色图
atmCTmat.txt
-1 // 定义片段
0
frag.txt
1 // 绘图
效果:
一般认为如果跃迁偶极矩矩阵热图与电荷转移矩阵热图出现定性区别时,电荷转移矩阵结果更值得采信。
Ref: