Post

电子耦合积分

Posted Updated
By Bane Dysta
6 min read
电子耦合积分

理论背景

对于一个普通化学反应，过渡态理论 (Transition State Theory, TST)提供了一个强大的框架来理解其反应速率：

\[k_{TST} = \frac{k_B T}{h} e^{-\Delta G^\ddagger / k_B T}\]

TST的核心思想是反应物需要沿着一个或多个反应坐标，越过一个能量最高点——过渡态 (Transition State, TS)，才能转化为产物。TS点与反应物之间的能量差$\Delta G^\ddagger$被称为活化能，也就是反应能垒。TST对于描述多数涉及核重排的反应都非常成功，然而面对电子转移反应，TST理论就遇到了难题：

1

D + A → D⁺ + A⁻

在BO近似下，原子核与电子的运动是分离的，Franck-Condon Principle又指出电子的运动远快于原子核，即在当电荷转移反应完成的时间尺度，原子核是不会发生移动的。反应物与产物的电子态转变是在统一核构型完成的，过渡态的意义不再明确，因此TST理论便陷入了瓶颈。

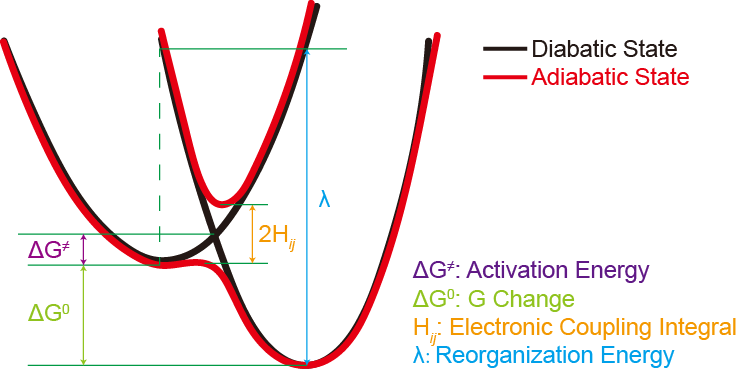
化学反应不像辐射跃迁，没有一个外来的光子给电子态提供激发能，所以限于FC原理的垂直跃迁要求，可以知道要发生电子转移反应，初末态的核坐标与电子能量均应当是相同的。基于这个思想，Rudolph A. Marcus提出了一个理论，用于描述电子转移反应。如果将反应坐标定义一个包含所有原子核运动的坐标，那么反应物与产物的势能面可以近似为两条抛物线(谐振近似)：

公式推导先跳过后面再补，总之就是有这么个关系：

\[\Delta G^\ddagger = \frac{(\lambda + \Delta G^0)^2}{4\lambda}\]

这个公式解决了活化能的问题，不过到达反应构型后，电子态的跃迁概率问题还没有解决。如果两个电子态之间没有耦合，那么即使到达反应构型也是不能发生跃迁的。于是引入了电子耦合积分$H_{ij}$来量化描述初态$\Psi_R$和末态$\Psi_P$的耦合：

\[H_{ij} = \langle \Psi_R | \hat{H} | \Psi_P \rangle\]

带着$H_{ij}$去算绝热态哈密顿量的本征值，会发现绝热态避免交叉劈裂的能量刚好是$2H_{ij}$。结合图像，可以看到电子耦合越强，沿绝热势能面往产物走越平滑，发生反应的速率自然越高。综合考虑了翻越能垒的核运动概率（指数项）和在垒顶发生跃迁的电子概率（指数前因子），Marcus理论给出了非绝热电子转移的最终速率公式：

\[k_{ET} = \frac{2\pi}{\hbar} |H_{AB}|^2 \frac{1}{\sqrt{4\pi\lambda k_B T}} \exp\left(-\frac{(\Delta G^0 + \lambda)^2}{4\lambda k_B T}\right)\]

最近笔者跟这个电子耦合积分磕上了，记录点计算方法。

Amesp

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

 ! CAM-B3LYP def2-svp
 >method
 cti on
 end
 >xyz 0 1
 O     -4.518266    -0.462976    -0.000025
 C     -3.373818    -0.080159     0.000051
 O     -2.382968    -1.014379    -0.000094
 C     -1.053391    -0.697723    -0.000076
 C     -0.126068    -1.734309    -0.000185
....
 H      5.020271    -0.532368     0.000460
 end
 >group
 1 16 -1 1
 17 25 1 1
 end

NWChem

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

start
charge 0
geometry noautosym
N                  3.09475022    0.16339201    0.00000400
C                  4.05193429   -0.91818206    0.00047300
C                  3.54813725    1.53366911   -0.00041700
...
H                 -3.70438027    2.06604515    0.00020400
end
basis
* library 6-31G*
end

dft
 # ET requests only uhf/odft input
 odft
 mult 1
 XC b3lyp
 mulliken
 vectors output C6Ngs.movecs
end
task dft

dft
 # ET requests only uhf/odft input
 odft
 mult 1
 XC b3lyp
 mulliken
 convergence nolevelshifting
 cdft 1 9 charge 1 pop Lowdin
 vectors output C6Nct.movecs
end
task dft

et
 vectors reactants C6Ngs.movecs
 vectors products C6Nct.movecs
end
task scf et

ref:

CP2K

相关资料

Reference

Quantum Chemistry
This post is licensed under CC BY 4.0 by the author.
Total hits!