为什么氯气与氢气的反应需要镁条引发？

Posted Jan 3, 2026 Updated Feb 15, 2026

By Bane Dysta

21 min read

为什么氯气与氢气的反应需要镁条引发？

假期刷到初中的一个实验的视频，氯气和氢气在光照下化合。想起当时很不能理解明明室内开了灯，但是不能发生反应，非要镁条点一下才行。曾经问老师得到的解释是灯光强度不够，要Mg点燃的时候那个晃眼的强度才行。现在掌握的知识多了些，忽然有兴致随便算算玩玩。

首先分析一下。反应的关键是氯氯键需要被光打断，解离成氯自由基。这个过程涉及到氯气的激发和断键，应该是吸收到S1然后过MECI断键。既然涉及到吸收，那首先需要了解一下自然光的光谱。日常生活里，常见的光基本上有两种：

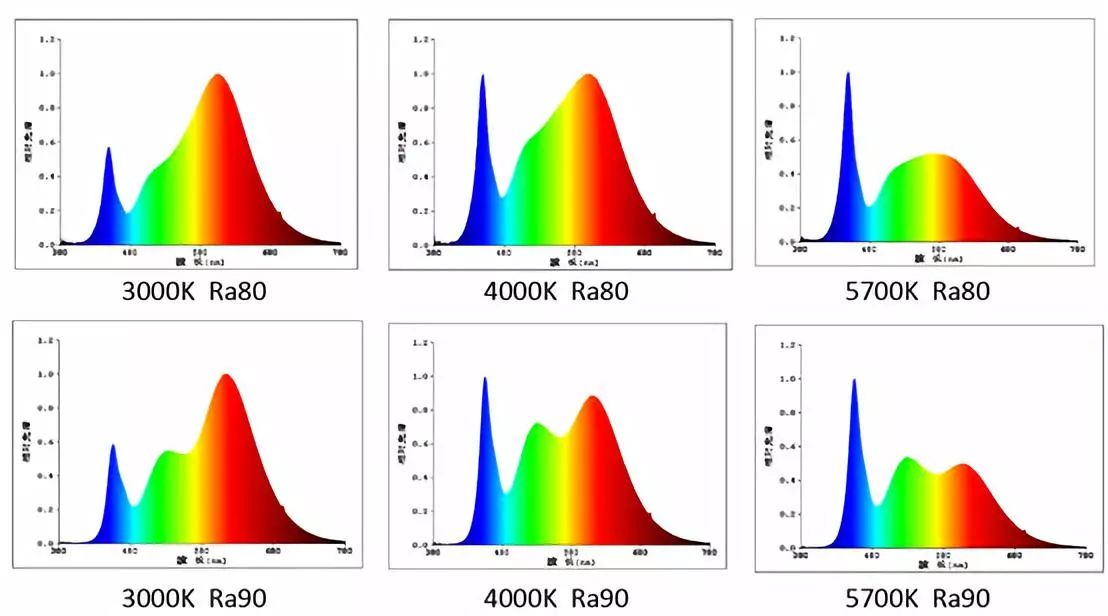
i. LED电灯。为了避免紫外辐射对人眼和材料的伤害，商业LED灯通常会滤掉紫外成分。找了些发射光谱，看到它的发射大概在450-700 nm之间，其中450 nm有一个尖锐的峰，再往蓝走强度锐减，400 nm以前基本都没有了。
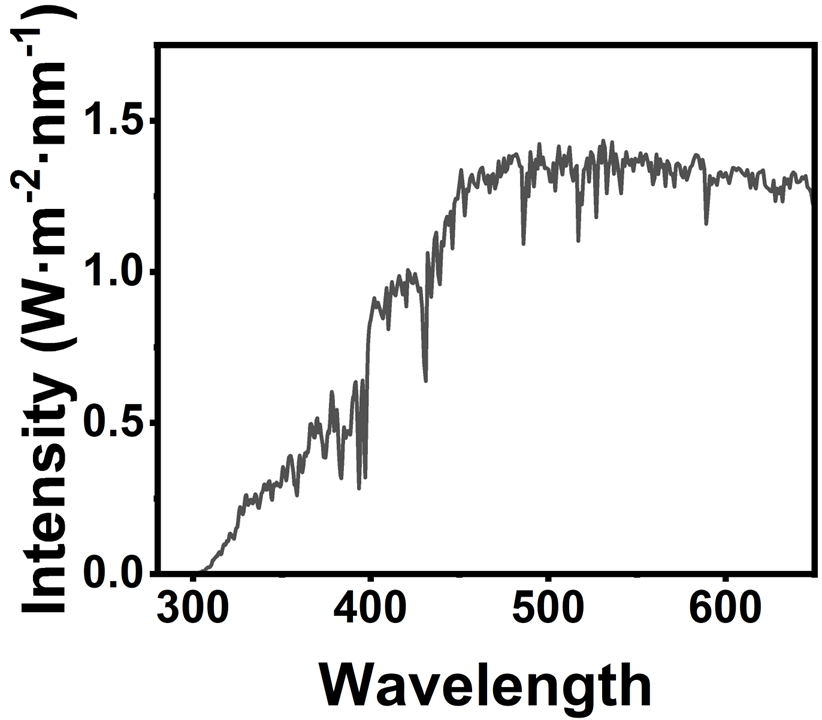
ii. 日光。取ASTM G-173¹的数据，太阳光到达地面的光谱(节选)大概长这样：
虽然紫外段的强度低些，但320 nm以上的光算是都有。

氯氯键的经典键能在242.6 kJ/mol，对应波长495 nm。那似乎确实这两种光都可以引发反应。但是笔者还是觉得有点奇怪，为什么自由基反应大多都要强调日光，而Mg又凭什么可以？

氯气的吸收

体系很小，CCSD优化一下键长看看：

%nproc=32
%mem=96GB
%chk=cl2.chk
# CCSD/def2tzvp opt freq=num

bane

0 1
Cl 0.0 0.0 0.0
Cl 0.0 0.0 2.00

换了三个基组测试：

基组	键长
def2-tzvp	2.00277
cc-pvtz	2.00943
def2-qzvp	1.98850

查到实验值是1.988，qzvp的结果还挺接近的，后面用这个键长当作平衡键长值了。

接着用NEVPT2算激发能。算简单的结构，直接交给MOKIT其实挺稳的，事后检查基本都没啥问题

%nproc=32
%mem=96GB
# NEVPT2/cc-pvtz

mokit{Nstates=2}

0 1
Cl      0.000000      0.000000      0.994248
Cl      0.000000      0.000000     -0.994248

这里MOKIT取的应该是CIS的NO作为初猜

CIS energies from Gaussian:
Excited State   1: E=   -918.836438 a.u. (  4.42 eV), f=0.0000, <S**2>=   0.000
Excited State   2: E=   -918.836438 a.u. (  4.42 eV), f=0.0000, <S**2>=   0.000
State-averaged NO generated using states 0~2.

MOKIT判断活性空间取(4e,3o)就够，看起来也确实是这样：

orb index	type	occ
20	Virtual	0.0006
19	Virtual	0.0061
18	Virtual	0.7899
17	Occupied	1.6046
16	Occupied	1.6046
15	Occupied	1.9964
14	Occupied	1.9964
13	Occupied	1.9990

NEVPT2计算结果：

SA-CASSCF(4e,3o) using program pyscf
$python Cl2_mokit_CIS_NO_SA-CAS.py >Cl2_mokit_CIS_NO_SA-CAS.out 2>&1
CASCI energies after SA-CASSCF(0 for ground state):   E_ex/eV   fosc
State   0, E =   -918.99823059 a.u. <S**2> = 0.000
State   1, E =   -918.83264461 a.u. <S**2> = 0.000    4.506   0.0011
State   2, E =   -918.83264461 a.u. <S**2> = 0.000    4.506   0.0011

NEVPT2 energies:                     E_ex/eV
State   0, E =   -919.44884920 a.u.
State   1, E =   -919.30884747 a.u.    3.810
State   2, E =   -919.30884747 a.u.    3.810

不过，如果要按照物理直觉的话，应该把3p全都拿进活性空间，也就是(10e,6o)，那么可以指定：

%nproc=32
%mem=96GB
# NEVPT2(10,6)/cc-pvtz

mokit{Nstates=2}

0 1
Cl      0.000000      0.000000      0.994248
Cl      0.000000      0.000000     -0.994248

MOKIT会提示你(4e,3o)就够，但也会按照你指定的来扩展：

Warning: SA-CAS(4e,3o) recommended, but you specify SA-CAS(10e,6o). Trying to fulfill...

...

OK, fulfilled.

...

SA-CASSCF(10e,6o) using program pyscf
$python Cl2_106_CIS_NO_SA-CAS.py >Cl2_106_CIS_NO_SA-CAS.out 2>&1
CASCI energies after SA-CASSCF(0 for ground state):   E_ex/eV   fosc
State   0, E =   -919.01499298 a.u. <S**2> = 0.000
State   1, E =   -918.85755861 a.u. <S**2> = 0.000    4.284   0.0008
State   2, E =   -918.85755861 a.u. <S**2> = 0.000    4.284   0.0008

NEVPT2 energies:                     E_ex/eV
State   0, E =   -919.42423482 a.u.
State   1, E =   -919.27994084 a.u.    3.926
State   2, E =   -919.27994084 a.u.    3.926

可以看到用自动判断的和手动指定的活性空间都算出了简并的$^1\Pi_u$态²。用(10e,6o)算的激发能是3.925 eV，比(4e,3o)的3.810 eV稍高。搜到exp：3.76 eV，这样看反而是(4e,3o)更接近实验值。不过此处没考虑Spin-Orbit Coupling，这个还会进一步降低$^1\Pi_u$的能量，外加NEVPT2也会略微高估激发能，(4e,3o)可能有些误差抵消的运气成分在。

我们还是取符合物理直觉的(10e,6o)，不然不好统一活性空间。其激发能对应波长316 nm，在很蓝的位置。

解离势能面

做个scan看看势能面是不是跟笔者先前推测的一样会走一个CI。这里笔者把$^3\Pi_u$态也算了，检查下有没有MECP，产生别的解离通道。

  
#!/bin/bash

# --- 参数设置区域 ---
R_eq=1.9885    # 起始键长
step=0.05      # 步长
n_points=35    # 总点数
base_name="Cl2"
list_file="scan_info.txt"  # 记录列表的文件名
# ------------------

# 1. 初始化列表文件，写入表头
# 使用 printf 保证表头对齐
printf "%-10s %-15s %-20s\n" "Point_ID" "Distance(A)" "Filename" > "$list_file"

for ((i=1; i<=n_points; i++))
do
    # 计算当前键长
    current_L=$(awk -v r="$R_eq" -v s="$step" -v i="$i" 'BEGIN {printf "%.4f", r + (i-1)*s}')
    
    # 生成文件名
    file_id=$(printf "%03d" $i)
    filename="${base_name}_${file_id}.gjf"

    # 生成输入文件
    cat > "$filename" <<EOF
%nproc=32
%mem=96GB
# NEVPT2(10,6)/cc-pvtz

mokit{Nstates=4,mixedspin}

0 1
Cl 0.0 0.0 0.0
Cl 0.0 0.0 $current_L

EOF

    # 2. 将信息追加到列表文件中
    # 这里的 %-10s 等是为了让文本列对齐，看起来更舒服
    printf "%-10s %-15s %-20s\n" "$file_id" "$current_L" "$filename" >> "$list_file"

    echo "已生成: $filename"
done

echo "----------------------------------------"
echo "所有文件已生成，键长列表已保存在: $list_file"

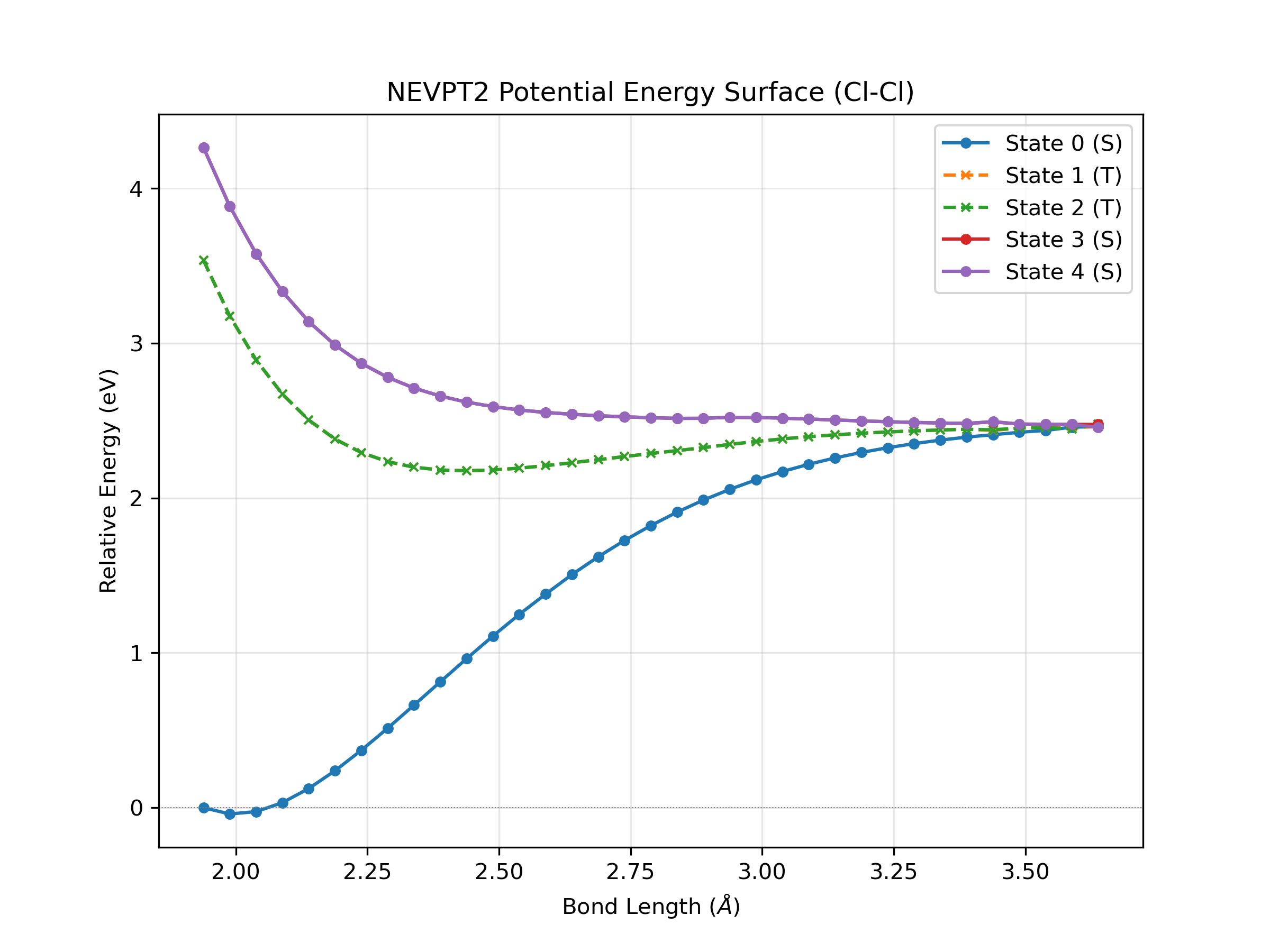
计算完成后，画个PES。绘图脚本太长就不贴了，读者可自行下载。PES长这样：

可以看到，三重态的能量始终比单重态没低多少。进一步计算SOC：

%pal nprocs 16 end
%maxcore 6000
! CASSCF VeryTightSCF
%casscf
 nel 10
 norb 6
 mult 1,3
 nroots 3,2
 maxiter 200
 CI MaxIter 200 NGuessMat 1000 end
 rel dosoc true PrintLevel 2 end
 PTMethod SC_NEVPT2
end
%method
 FrozenCore FC_NONE
end
%scf
 Thresh 1e-12
 Tcut 1e-14
 CNVDamp False
end

先看一眼能量跟之pyscf计算值能不能对上，以确认两个程序是不是收敛到相同的解

-----------------------------
 NEVPT2 TRANSITION ENERGIES
------------------------------

LOWEST ROOT (ROOT 0, MULT 1) =   -919.424605715 Eh -25018.815 eV

STATE ROOT MULT  DE/a.u.     DE/eV    DE/cm**-1
   1:   0    3   0.118301     3.219  25964.2
   2:   1    3   0.118301     3.219  25964.2
   3:   1    1   0.144301     3.927  31670.5
   4:   2    1   0.144301     3.927  31670.5

对比pyscf结果，可以看到基本一致

NEVPT2 energies:                     E_ex/eV
State   0, E =   -919.42452578 a.u.
State   1, E =   -919.30635102 a.u.    3.216
State   2, E =   -919.30635102 a.u.    3.216
State   3, E =   -919.28030095 a.u.    3.925
State   4, E =   -919.28030095 a.u.    3.925

读取旋轨耦合，得S1/T1的socme值为106.47 cm-1。这个值是相当大的，说明这个ISC可以发生。从PES的形状上看，$^3\Pi_u$在2.35埃左右有个极小点，可能是因为同自旋的组合让$\sigma_{3p}^*$轨道削弱氯氯键的效应没那么强，允许氯气以一个弱键的形式存在。这是一个不利于解离的因素。

但也应当注意到这里的势垒非常低。笔者之前看过些研究MECI的文献，有一种意见是MECP点的能垒应当用E(MECP)-E(FC)而不是E(MECP)-E(S1)，笔者的理解是FC点弛豫到S1极小点时还会带着动能，很容易走到势能面另一边相同势能的位置，所以这部分能垒不算数：

J. Phys. Chem. Lett. 2020, 11, 7790−7797

参考文献说法，氯气这个能垒理论上非常容易跨过去，走到三态交叉点还是很容易的。同时，注意到S0/T1的socme为0，因此从T1直接跃迁回S0要靠HT效应，在数量级上不会比进入MECP的速率更高，最终还是会解离。

综上，氯气的光解大概两条路径：

直接从FC点沿$^1\Pi_u$势能面弛豫到MECP点
先通过ISC到$^3\Pi_u$，再跨过一个很浅的势垒走到MECP点

而这一切的前提都是，氯气需要被激发到$^1\Pi_u$态。

Mg的发射

接下来看看镁条的发射。Mg燃烧的时候温度非常高，可以通过热激发来到$^1P_1$态³，我们看看它的发射是什么样。Mg的活性空间应该是3s电子和3s+3p轨道，也就是(2e,4o)。从3s向任意一个3p激发，应当是三重简并的，所以SA-CAS平均基态和三个激发态：

%nproc=32
%mem=96GB
# NEVPT2(2,4)/aug-cc-pvtz

mokit{Nstates=3}

0 1
Mg      0.000000      0.000000      0.000000

得到激发能4.326 eV，换算波长285 nm，明显属于紫外发射。（搜到exp：4.436 eV，算是对的不错了）

SA-CASSCF(2e,4o) using program pyscf
$python Mg_CIS_NO_SA-CAS.py >Mg_CIS_NO_SA-CAS.out 2>&1
CASCI energies after SA-CASSCF(0 for ground state):   E_ex/eV   fosc
State   0, E =   -199.61202158 a.u. <S**2> = 0.000
State   1, E =   -199.46722928 a.u. <S**2> = 0.000    3.940   0.3976
State   2, E =   -199.46722906 a.u. <S**2> = 0.000    3.940   0.3976
State   3, E =   -199.46722880 a.u. <S**2> = 0.000    3.940   0.3976

NEVPT2 energies:                     E_ex/eV
State   0, E =   -199.65822267 a.u.
State   1, E =   -199.49923536 a.u.    4.326
State   2, E =   -199.49923561 a.u.    4.326
State   3, E =   -199.49923568 a.u.    4.326

注意到振子强度有0.3976，说明Mg在285 nm这个发射比较强。

但是这里有个新问题，Mg的发射峰在4.326 eV，Cl2的吸收峰在3.925 eV，这差了0.4 eV还是不小的，真的能匹配吗？笔者提出两个猜测：

i. 氯气有个更高的激发态，能量恰好在4.3 eV附近
ii. $^1\Pi_u$态的吸收带可以展到285 nm(4.3 eV)附近

这里先简单排除一下猜想1：

NEVPT2 energies:                     E_ex/eV
State   0, E =   -919.42362289 a.u.
State   1, E =   -919.27946423 a.u.    3.923
State   2, E =   -919.27946422 a.u.    3.923
State   3, E =   -919.17361624 a.u.    6.803
State   4, E =   -919.17361624 a.u.    6.803

后面的态能量的有点太高了，所以大概是第二种原因，接下来验证一下。

吸收光谱

吸收峰已经有了，这里可以选择用高斯函数展出来一个模拟光谱，但我们最终的目的是找到引发氯气解离的光谱范围，FWHM随意取好像不太好。不过这个分子只有一个正则模式，而且前面freq=num已经算了频率值是561.4278 cm-1（exp:560 cm-1左右，对的不错）。于是这里可以玩点花的。首先基于力常数做个Wigner采样：

  
import numpy as np
import os

# ================= 配置 =================
# 输入参数
freq_cm = 561.4           # 频率 (cm^-1)
mass_amu = 35.45          # 相对原子质量
r_eq = 1.9885             # 平衡键长
temp = 298.15             # 温度 (K)
n_samples = 200           # 采样数量

# 计算设置
nproc = 32
mem = "96GB"
route_section = "# NEVPT2(10,6)/cc-pvtz"
mokit_options = "mokit{Nstates=2}"
output_dir = "gjf_inputs" # 输出目录

# ================= 采样 =================
# 物理常数与 Wigner 采样参数
h_bar = 1.0545718e-34    # J*s
c = 2.99792458e10        # cm/s
amu_to_kg = 1.660539e-27 # kg
k_B = 1.380649e-23       # J/K

mu = (mass_amu * amu_to_kg) / 2.0
omega = freq_cm * 2 * np.pi * c 

sigma_0k = np.sqrt(h_bar / (2 * mu * omega))
if temp == 0:
    correction_factor = 1.0
else:
    exponent = (h_bar * omega) / (2 * k_B * temp)
    correction_factor = np.sqrt(1.0 / np.tanh(exponent))

sigma_r_meter = sigma_0k * correction_factor
sigma_r_ang = sigma_r_meter * 1e10

# Wigner采样并排序
deltas = np.random.normal(0, sigma_r_ang, n_samples)
bond_lengths = np.sort(r_eq + deltas)

print(f"--- Wigner 采样信息 ---")
print(f"温度: {temp} K")
print(f"频率: {freq_cm} cm^-1")
print(f"键长标准差 (Sigma): {sigma_r_ang:.4f} Å")
print(f"生成样本数: {n_samples}")
print("-" * 30)

# ================= 计算 =================
os.makedirs(output_dir, exist_ok=True)

for i, r in enumerate(bond_lengths):
    # 格式化索引，200个文件建议用三位数字补零 (001, 002...) 方便排序
    index = i + 1
    filename = f"Cl2_point{index:03d}.gjf"
    filepath = os.path.join(output_dir, filename)
    
    # 构建文件内容
    content = f"""%nproc={nproc}
%mem={mem}
{route_section}

{mokit_options}

0 1
Cl      0.000000      0.000000      0.000000
Cl      0.000000      0.000000      {r:.6f}

""" 
    # 写入文件
    with open(filepath, 'w') as f:
        f.write(content)

    # 仅打印前几个和后几个作为进度提示，避免刷屏
    if i < 3 or i >= n_samples - 3:
        print(f"Generated: {filepath} (R = {r:.4f} Å)")
    elif i == 3:
        print("...")

print("-" * 30)
print(f"全部完成！文件已保存在 {output_dir}/ 目录下。")

随后运行计算并绘图。这里因为NEVPT2不输出振子强度，笔者用了CASCI的振子强度凑合。绘图脚本很长，不贴在这里了，读者可自行下载。

python spectrum.py

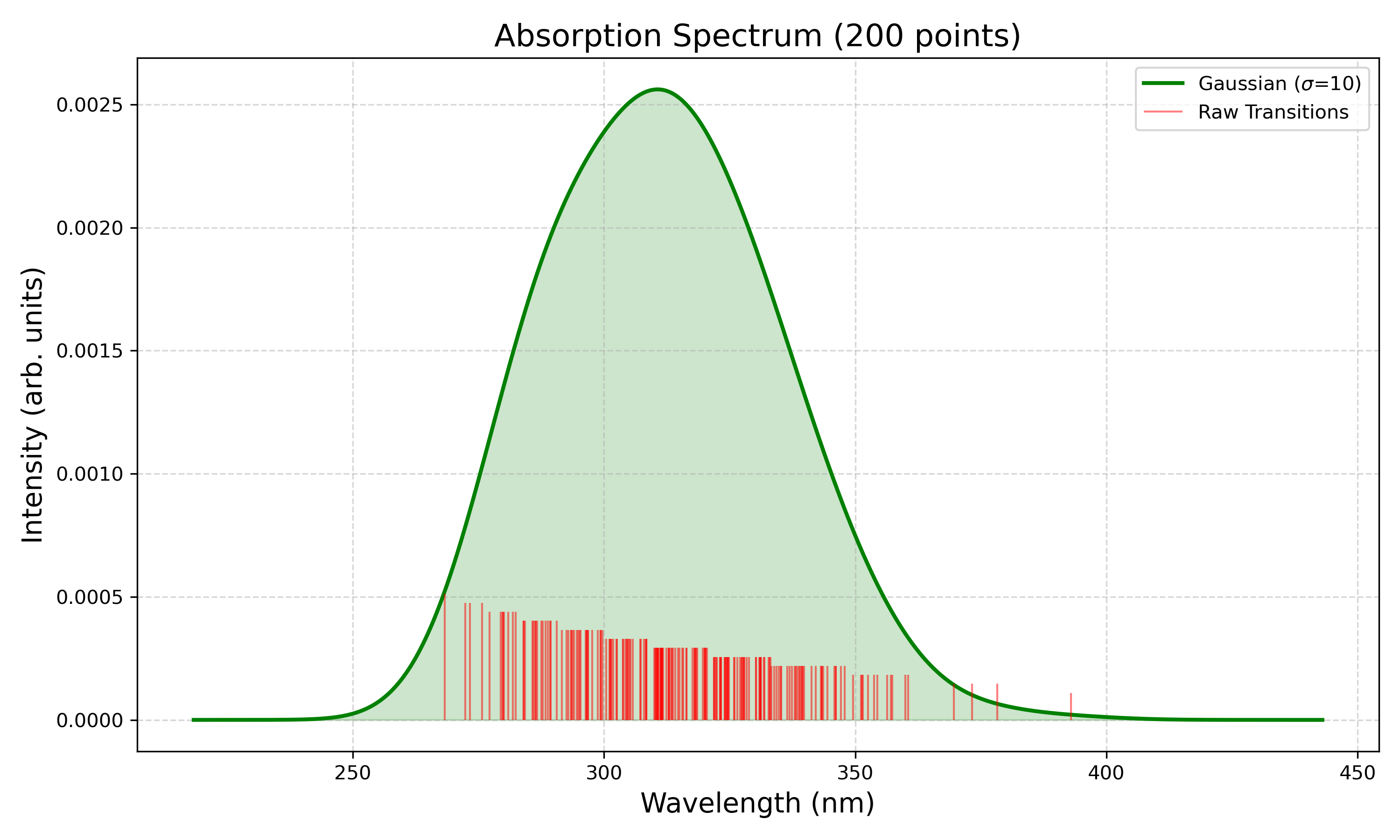
我们看最终的光谱：

从光谱形状上看，$^1\Pi_u$态从250 nm开始有吸收，到400 nm为止，主要的吸收带大概在275-340 nm。搜了个实验光谱(下图紫线)。注意到模拟的光谱250 nm处吸收的提升速度略快于实验光谱，这可能是NEVPT2轻微高估激发能引起的。除此之外，特征非常接近。 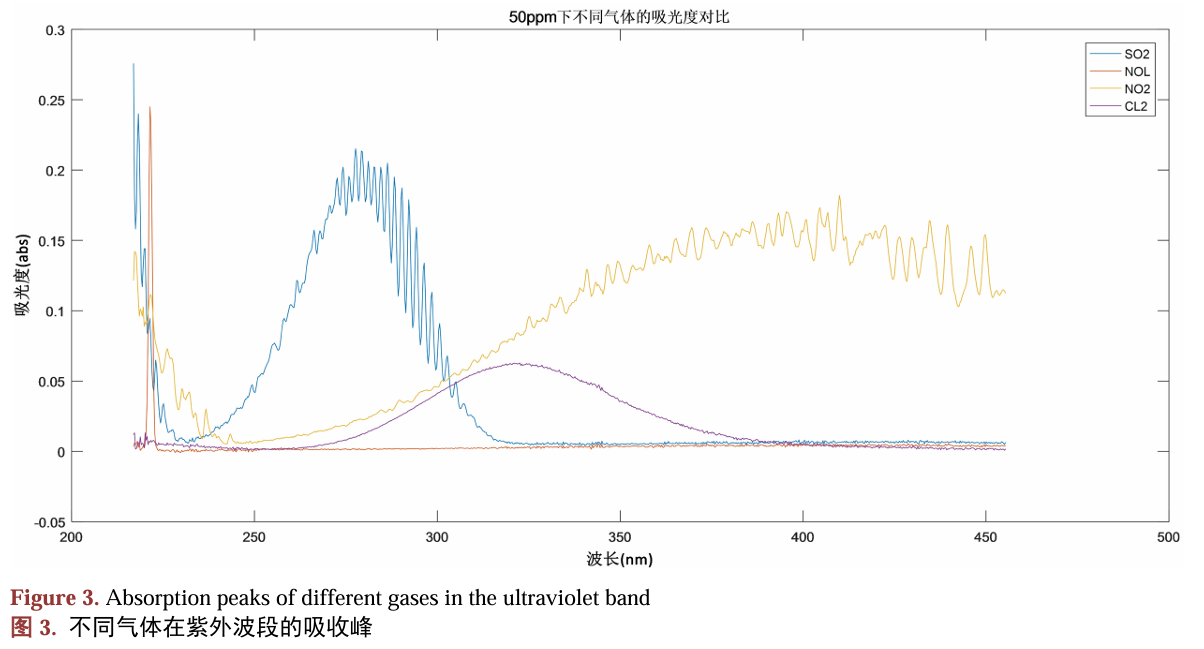阎杰, 夏赛, 程鹏, 陈民旺. 基于差分吸收光谱技术的氯气在线监测系统研制[J]. 应用物理, 2023, 13(11): 421-429.

结论

结合前面的信息，可以总结如下：

镁的强发射在285 nm，恰好落在此范围内，是引发此反应很好的选择。
自然光在此范围的辐射强度比可见区弱了5、6倍，而且由于普通玻璃会吸收紫外线，能够透过窗户到达反应容器的会更少，笔者觉得想像镁一样引发这个反应到爆炸的程度可能不太容易，估计那时候可见光都开始晃眼了。
LED电灯的发射峰在450 nm，虽然能量高于氯气的键能，但氯气在400以上吸收只能靠$^3\Pi_u$的禁阻吸收(氯气呈淡黄绿色的原因)，吸收截面非常非常小，而电灯在400以下也基本无发射，想引发这个反应是非常困难的。

ASTM G-173是一个比较常用的太阳光谱实验测试数据，Gemini称这是“标准太阳光”。笔者在NREL官网找到了这个数据：Reference Air Mass 1.5 Spectra ↩︎
$^1\Pi_u$ 是一个分子谱项记号，左上角的$^1$指单重态；$\Pi$ 是旋转对称性记号，指角动量投影$\Lambda=1$；右下角的$u$是反演对称性记号，$u$是奇宇称。来历：氯气的第一激发态是H→L的跃迁，根据分子轨道理论，氯气的FMO分子轨道能量顺序是 $ \sigma_{3s} < \sigma_{3s}^* < \sigma_{3p} < \pi_{3p} < \pi_{3p}^* < \sigma_{3p}^* $。填充14个价电子后，HOMO轨道是二重简并的$\pi_{3p}^* $(这也是$^1\Pi_u$态二重简并的原因)，而LUMO轨道是$\sigma_{3p}^* $。$\sigma$轨道的轨道角动量是0，$\pi$轨道的轨道角动量是±1，最终$\Lambda=1$，为$\Pi$态。$\sigma$轨道是偶宇称，$\pi$轨道是奇宇称，所以这个态也是奇宇称。 ↩︎
$^1P_1$是一个原子谱项记号，左上角的$^1$依然指单重态($S=0$)；$P$是指轨道角动量$L=1$；右下角则是总角动量$J$，$J=L+S=1$。 ↩︎

excited state MOKIT

This post is licensed under CC BY 4.0 by the author.

氯气的吸收

解离势能面

Mg的发射

吸收光谱

结论

Trending Tags