Study note:量子化学方法
笔者是初学者,理解可能有误,以下内容请慎重相信。
1 Hartree-Fock方法 (HF)
Hartree-Fock方法是一种多电子近似方法,核心思想是将复杂的多电子波函数转化为简单的单电子问题,并通过自洽场方法迭代求解波函数和能量。
a. 独立粒子近似
假设电子运动是独立的,即每个电子在其余电子生成的平均场中运动。这样多电子波函数可近似为由一组单电子波函数的线性组合构成,用Slater行列式来表示:
其中:$\Psi_{\text{HF}}$是HF波函数;$\psi_i$是单电子轨道;$N$是电子数。
b. Hartree-Fock方程
首先定义描述单电子运动的Fock算符:
其中:$h$为单电子哈密顿量,包括动能和核吸引部分;$\hat{J}$为库仑相关算符;$\hat{K}$为交换算符。
单电子轨道满足如下本征方程:
\[F \psi_i = E_i \psi_i\]其中:$E_i$为单电子轨道能量;$\psi_i$为单电子波函数
c. 自洽场(SCF)迭代
- 首先通过一些方法构建初猜轨道,如SAD法、Hückel法等,并计算Fock算符
- 通过基函数展开Hartree-Fock方程,解出轨道系数和轨道能量
- 通过解出的轨道系数构造新的轨道,利用新轨道计算电子分布,更新Fock算符
- 重复该流程,直到分子轨道和能量收敛。
自洽场收敛后,就得到了体系的HF能量。观察Fock算符的构造,可以发现由于使用了平均场近似,HF方法对于电子的相关作用的描述非常粗糙。
2 post HF方法
HF不擅长描述电子相关作用,因此后来基于HF波函数又开发了许多方法。
微扰理论 (Møller-Plesset Perturbation Theory, MP)
Møller-Plesset微扰理论的目标是通过对电子波函数和能量的逐阶修正来描述电子相关效应,核心思想为将哈密顿算符中难以求解的电子相关部分提取出来,作为微扰项处理:
\[\hat{H} = \hat{H_0} + \lambda\hat{H'}\]其中:
- $\hat{H_0}$为HF哈密顿量
$\hat{H’}$为微扰项,它可以表示为:
\[\hat{H}' = \hat{H}_{\text{ee}} - \hat{V}_{\text{HF}},\]其中:
- $\hat{H}_{\text{ee}}$ 是电子之间的精确相互作用;
- $\hat{V}_{\text{HF}}$ 是 HF 的平均场近似下的电子相互作用。
使用微扰参数 $\lambda$ 将总能量和波函数展开为级数:
\[E = E_0 + \lambda E_1 + \lambda^2 E_2 + \lambda^3 E_3 + \cdots,\] \[|\Psi\rangle = |\Psi_0\rangle + \lambda |\Psi_1\rangle + \lambda^2 |\Psi_2\rangle + \cdots.\]其中:
- 零阶项$E_0$为HF能量,即 $\langle\Psi_0|\hat{H}_0|\Psi_0\rangle$
- 由于HF波函数使用了变分法,一阶项$E_1$为0。
二阶项$E_2$可以写为:
\[E_2 = \sum_{i \neq 0} \frac{|\langle \Psi_0 | \hat{H}' | \Psi_i \rangle|^2}{E_0 - E_i}\]在实际计算中,二阶能量校正的表达式可以写为:
\[E_2 = \sum_{ij}^{\text{occupied}} \sum_{ab}^{\text{virtual}} \frac{| \langle ij | ab \rangle - \langle ij | ba \rangle |^2}{\epsilon_i + \epsilon_j - \epsilon_a - \epsilon_b}\]其中:
- $i, j$:占据轨道(HF 波函数中被填满的轨道)。
- $a, b$:虚轨道(HF 波函数中未被填满的轨道)。
- $\epsilon_i, \epsilon_j, \epsilon_a, \epsilon_b$:HF 轨道能量。
- $\langle ij | ab \rangle$:双电子积分,表示两个电子在占据轨道 $i, j$ 和虚轨道 $a, b$ 之间的相互作用。
最常用的微扰方法为MP2,更高阶的方法由于形式复杂,计算代价较大,并不常用。
组态相互作用 (Configuration Interaction, CI)
CI是一种多电子波函数近似方法,核心思想是通过线性组合多个单电子波函数来表示体系的真实波函数,以避免使用平均场近似处理电子相关问题。
就像用多个共振式共同描述体系的真实结构一样,体系的真实波函数也可以被表示为多个Slater行列式的线性组合:
\[\Psi_{\text{CI}} = c_0 \Phi_0 + \sum_i c_i \Phi_i + \sum_{i<j} c_{ij} \Phi_{ij} + \cdots\]其中:
- $\Phi_0$ 是参考态波函数,通常为HF波函数。
- $\Phi_i, \Phi_{ij}, \dots$ 是通过单电子、双电子等激发生成的激发组态。
- $c_0, c_i, c_{ij}, \dots$ 是各个组态的系数。
CI的目标是通过变分原理最小化总能量,因此需要构造哈密顿矩阵 $H_{\text{CI}}$,矩阵元定义为: \(H_{ij} = \langle \Phi_i | \hat{H} | \Phi_j \rangle,\) 其中:$\hat{H}$ 是全电子哈密顿算符;$\Phi_i$ 和 $\Phi_j$ 是不同组态的 Slater 行列式。
随后通过对CI哈密顿矩阵的对角化,可以得到体系的基态和激发态波函数与能量。然而,完全考虑所有组态时,计算复杂度将达到$O(N!)$,计算量随体系增大而爆炸式增长,仅适用于极小体系。因此,实际使用的CI多数为截断CI,如仅包含一阶项的CIS、考虑到二阶项的CISD等。
耦合簇 (Coupled Cluster, CC)
为了避免显示计算CI的行列式系数,提出了Coupled Cluster方法。该方法的核心思想是通过指数形式的簇算符$e^{\hat{T}}$描述体系激发,并通过指数函数的泰勒展开将高阶激发纳入考虑:
\(|\Psi_{\text{CC}}\rangle = e^{\hat{T}} |\Phi_0\rangle,\) 其中:
- $\Phi_0$ 是参考态波函数,通常为HF波函数。
$\hat{T}$ 是激发算符,定义为: \(\hat{T} = \hat{T}_1 + \hat{T}_2 + \hat{T}_3 + \dots,\)
$\hat{T}_1, \hat{T}_2$ 等算符用于描述不同阶的电子跃迁。比如:
\[\hat{T}_1 = \sum_{ia} t_i^a a_a^\dagger a_i\] \[\quad \hat{T}_2 = \frac{1}{4} \sum_{ijab} t_{ij}^{ab} a_a^\dagger a_b^\dagger a_j a_i,\]其中:
- $t_i^a$ 和 $t_{ij}^{ab}$ 为激发振幅,可以调整激发态的组态系数。
- $a_a^\dagger, a_i$ 为创建和湮灭算符,分别对应占据和虚轨道。
体系总能量为:
\[E_{\text{CC}} = \langle \Phi_0 | \hat{H} e^{\hat{T}} | \Phi_0 \rangle.\]将 Schrödinger 方程投影到不同的组态空间,得到一系列关于激发振幅 $t_i^a, t_{ij}^{ab}$ 等的非线性方程组:
\[\langle \Phi_i^a | \hat{H} e^{\hat{T}} | \Phi_0 \rangle = 0, \quad \langle \Phi_{ij}^{ab} | \hat{H} e^{\hat{T}} | \Phi_0 \rangle = 0, \dots\]最后通过数值迭代求解这些振幅方程,求得正确的振幅值后,该等式将会成立,就可以得到体系能量了。
CC的优点是避免了显示计算组态系数,通过指数的泰勒展开和激发振幅来构造了等效的表示方法,只要考虑到二阶项就能得到很高精度的结果。缺点是需要解非线性方程,可能带来数值收敛性问题。
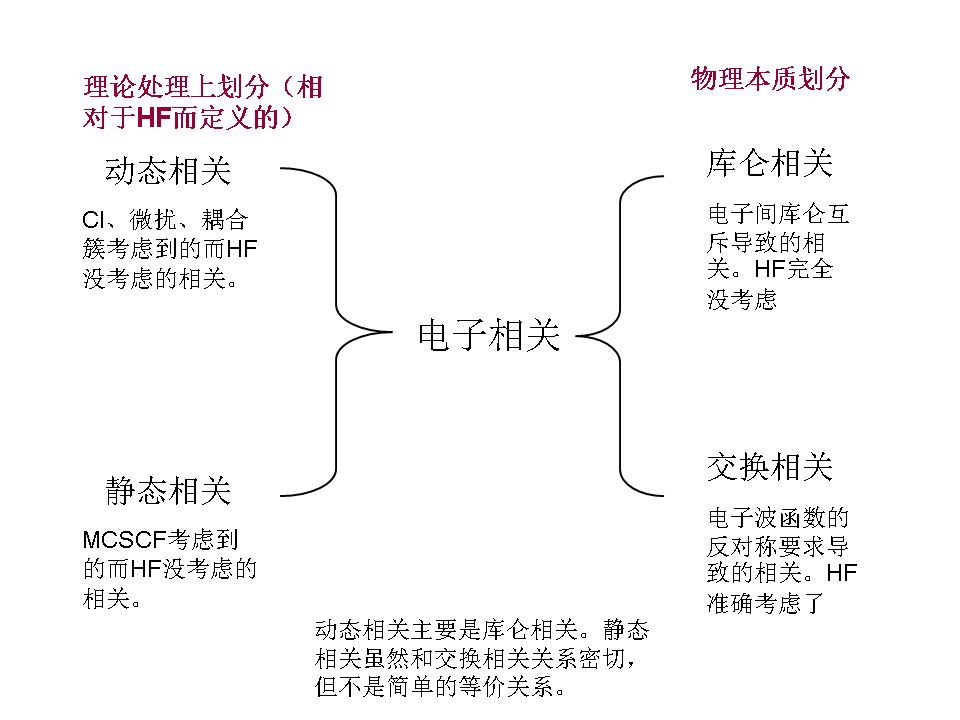
3 多参考组态自洽场 (Multi-Configurational Self-Consistent Field, MCSCF)
上述方法着眼于解决动态相关问题,然而除高阶CI和高阶CC以外,这些方法对静态相关的考虑比较欠缺。因此当HF波函数对体系描述存在定性错误时,上述方法除高阶CI和高阶CC外均会失效。MCSCF方法是一种针对多电子体系的量子化学方法,用于精确描述静态相关效应,核心思想是直接优化多电子波函数,从而更好地描述静态相关效应。
完整活性空间自洽场(Complete Active Space Self-Consistent Field, CASSCF)
CASSCF方法是MCSCF的经典实现之一,广泛用于研究分子基态和低激发态的电子结构。其核心思想是定义一个完整活性空间(Complete Active Space, CAS),在活性空间内进行FCI处理,考虑所有电子组态:
\[\Psi_{\text{CASSCF}} = \sum_i c_i \Phi_i,\]其中:
- $\Phi_i$ 是活性空间内不同电子组态的Slater行列式;
- $c_i$ 是每个组态的线性组合系数。
体系能量为:
\[E_{\text{CASSCF}} = \langle \Psi_{\text{CASSCF}} | \hat{H} | \Psi_{\text{CASSCF}} \rangle + V_\text{HF}\]其中:$V_\text{HF}$是活性空间外的电子在平均场近似下的能量。
交替优化$c_i$和$E_{\text{CASSCF}}$,直到二者均收敛,就能得到CASSCF级别的轨道和能量。
完整活性空间二阶微扰理论(Complete Active Space Perturbation Theory 2nd Order, CASPT2) 与N电子价态二阶微扰理论(N-Electron Valence Perturbation Theory 2nd Order, NEVPT2)
CASSCF对活性空间外的电子仍然使用平均场近似,因此对动态相关描述欠缺。CASPT2和NEVPT2是基于CASSCF波函数的二阶微扰理论方法,核心思想是通过MP2描述动态相关,从而得到更准确的能量。按照微扰理论,以CASSCF波函数为参考波函数将哈密顿量分解为零级哈密顿量和微扰哈密顿量:
\[\hat{H} = \hat{H}_0 + \hat{H}'.\]其中,动态相关的贡献通过二阶微扰能量校正计算得到: \(E^{(2)} = \sum_{k \neq 0} \frac{\langle \Psi_0 | \hat{H}' | \Psi_k \rangle^2}{E_0 - E_k}.\)
CASPT2和NVEPT2的区别在于NEVPT2对波函数和零阶哈密顿量的定义更加严格,所有修正能量满足正定性条件,结果往往更加准确。然而,NEVPT2的形式更复杂,计算效率不如CASPT2。
MRCI、MRCC
类似地,以CASSCF波函数作为参考态,按照前述原理进行CI和CC计算,可以同时精确描述动态相关和静态相关效应。缺点是计算量极大,只能研究极小体系。
4 密度泛函理论(Density Functional Theory, DFT)
DFT是一种基于电子密度而非波函数的量子力学方法,起源于第一性原理,在量子化学方面同样表现出色。其核心思想是通过电子密度$\rho(\mathbf{r})$而非复杂的多电子波函数来描述多电子体系。
a. Hohenberg-Kohn定理
在外势 $v(\mathbf{r})$ 给定的条件下,体系的基态电子密度 $\rho(\mathbf{r})$ 可唯一确定体系的外势 $v(\mathbf{r})$ 和哈密顿量 $\hat{H}$,进而确定体系的基态波函数 $\Psi_0$ 和能量 $E_0$,即:$\rho(\mathbf{r}) \rightarrow v(\mathbf{r}) \rightarrow \Psi_0 \rightarrow E_0$。在HK定理下,3N维的多电子波函数可以被简化为3维的电子密度泛函,大大降低了计算复杂度。
b. Kohn-Sham方程
虽然经过简化,直接处理多电子体系的相互作用密度仍然非常复杂。Kohn和Sham提出了将问题转化为一组单电子问题的方法。首先,将真实的相互作用体系映射到一个无相互作用的虚拟体系,通过引入单电子轨道 $\phi_i(\mathbf{r})$ 表达电子密度:
\[\rho(\mathbf{r}) = \sum_i |\phi_i(\mathbf{r})|^2.\]然后通过以下Kohn-Sham方程计算单电子轨道:
\[\left[ -\frac{\hbar^2}{2m} \nabla^2 + v_{\text{eff}}(\mathbf{r}) \right] \phi_i(\mathbf{r}) = \epsilon_i \phi_i(\mathbf{r}),\]其中$v_{\text{eff}}(\mathbf{r})$ 是有效外势,包括库仑势和交换-相关势。库伦势由电子密度产生的电子-电子相互作用,可以精确求解;而交换-相关势是DFT最重要的部分,描述量子力学效应和电子相关。精确的交换-相关泛函形式未知,实际常用各种近似方法构造交换-相关泛函:
局域密度近似(Local Density Approximation, LDA)假设在均匀电子气模型下,交换-相关能仅依赖于局域的电子密度。LDA泛函的优点是形式简单,计算高效,缺点是对密度梯度大的体系(非金属体系)描述不够准确。例:SVWN
- 广义梯度近似(Generalized Gradient Approximation, GGA)虑了密度梯度对交换-相关能的修正,可以分别考虑交换部分和相关部分,提供更精确的结果。例:
- 交换泛函:B88 (Becke 1988)等。
- 相关泛函:LYP (Lee-Yang-Parr)等。
- 交换-相关泛函:BLYP、PBE等。
- 元广义梯度近似(meta-Generalized Gradient Approximation, meta-GGA)引入了电子动能密度或Laplacian等额外信息,可以更加细致地刻画复杂的电子相互作用。例:M06-L,TPSS等。
c. 杂化(Hybrid)
为了改进泛函性能,可以在交换相关项$E_{\text{XC}}$中引入其他理论方法。
- HF通过单电子波函数的反对称化Slater行列式反映电子间排斥的非局域性质,能够提供比DFT更准确的交换能量。使用一部分HF交换项代替DFT交换项,可以得到杂化泛函。例:B3LYP等。
- post-HF方法,如MP2等对电子相关描述较好,在杂化泛函的基础上引入MP2相关项,可以得到双杂化泛函。例:B2PLYP等。
构造出泛函后,可以像HF的自洽场方法一样迭代求解KS方程,直到电子密度收敛,就能得到DFT级别的能量。
5. 对比
| 方法 | 静态相关 | 动态相关 | 备注 |
|---|---|---|---|
| HF | 无法考虑 | 无法考虑 | |
| DFT | 可以考虑 | 描述较好 | 静态相关强的问题应使用纯泛函 |
| 单参考CI | 几乎没有考虑 | 描述较好 | 高阶CI一定程度上能解决静态相关问题 |
| 微扰 | 几乎没有考虑 | 可以考虑 | |
| 单参考CC | 几乎没有考虑 | 描述较好 | 高阶CC一定程度上能解决静态相关问题 |
| CASSCF | 描述较好 | 几乎没有考虑 | |
| NEVPT2、CASPT2 | 描述较好 | 描述较好 | |
| MRCC、MRCI | 描述较好 | 描述较好 |