Study note：Fluorescence Probe - part A
tips：荧光探针的机理很杂很碎，而错误解读又很多，难以分辨。本文记录一下笔者学习过程中对各种基本原理的总结，内容仅供参考，未必完全正确，会随笔者学习理解过程随时更新。如果读者发现任何地方与已有认识不符，不要怀疑，一定是笔者理解有误，请务必在评论区指出！
荧光过程可以用经典的Jablonski图来表示。简单来讲，基态分子可以吸收一个光子跃迁到激发态，随后通过快速内转换和振动弛豫回到第一激发态的最低振动能级，再释放一个光子回到基态。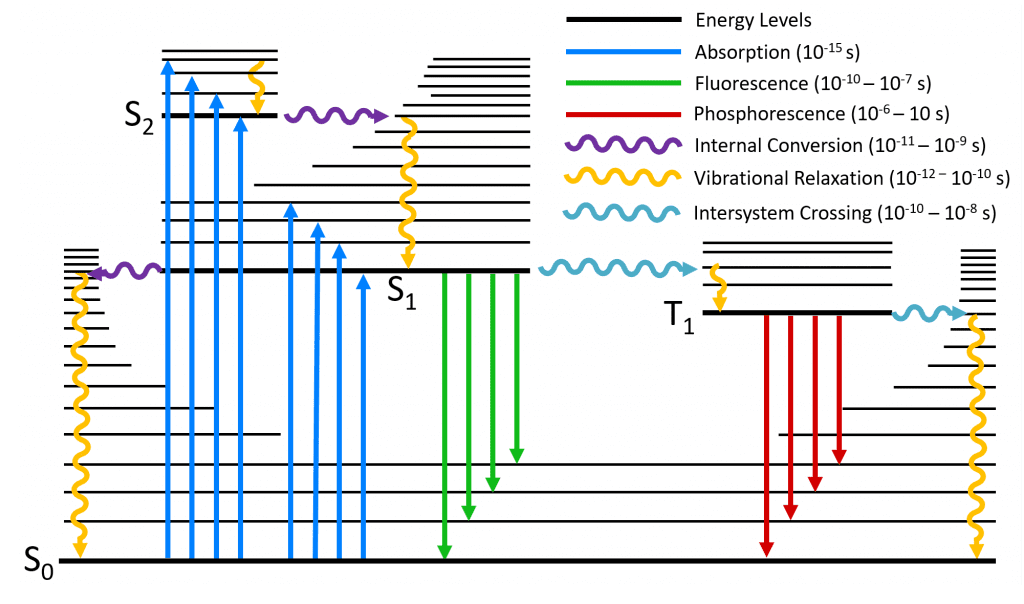 
这个能级图虽然很直观，但是几乎没有描述几何行为。为了更好地理解荧光，这里需要先引入势能面的概念。
1 势能面上的荧光
势能面（Potential Energy Surface, PES）描述了一个分子系统中原子之间相互作用势能随它们空间位置变化而变化的趋势。简单来说，在Born-Oppenheimer近似下，核运动的时间尺度上电子结构始终处于基态，因此势能面是体系势能关于核坐标的函数图像，描述了分子在不同的几何结构下的能量分布，可以用来分析分子的动力学和热力学行为：
\[V(\mathbf{R}) = \sum_{i=1}^N \sum_{j>i}^N V_{ij}(|\mathbf{R}_i - \mathbf{R}_j|)\]式中：
- $V(\mathbf{R})$ 为系统的总势能
- $V_{ij}$ 表示粒子$i$和粒子$j$之间的相互作用势，根据系统的具体特性可以采用不同的形式，如Morse势、Lennard-Jones势、库仑势等。
- $\mathbf{R}_i$ 和 $\mathbf{R}_j$ 分别是第$i$个和第$j$个粒子的位置向量
- $N$ 为系统中粒子的总数
可以发现，对于多原子分子来说，由于每个粒原子的三个坐标($x,y,z$)都会影响势能，一个N原子分子的每个电子态的势能面都有3N个自由度。除去不影响能量的整体平移和整体旋转，N原子分子的势能面将是3N-6维的超曲面。由于势能面的高维性，多原子分子的完整势能面是无法用图像或是常规手段进行描述的，实际研究中一般会选择某一个或几个反应坐标(Reaction Coordinate)进行研究。除了原子核以外，电子的分布也影响势能面的形状。不同的电子结构形成了不同的电子态，各个电子态都拥有各自的势能面。
正确分辨电子态与分子轨道的概念。分子轨道基于单电子近似产生，描述的是一块电子出现概率高的假想空间区域；而电子态描述的是分子中所有电子的整体结构和量子状态，考虑电子在所有分子轨道中的配置情况。我们通常讲的跃迁指的是从一个电子态转换到另一个电子态的过程，而不是单纯由某个轨道向另一个轨道转移1个电子——虽然后者对应的情况可能存在，但许多电子跃迁仅用单对轨道是无法准确描述的。
Jablonski图上的跃迁过程也可以完整地用势能面来表示，但初看时会比较凌乱，因此这里从一个简化的模型入手。假设谐振近似成立，则某反应坐标下的初态与末态(相对于初态平移了$Q_0$)势能面的表达式分别为：
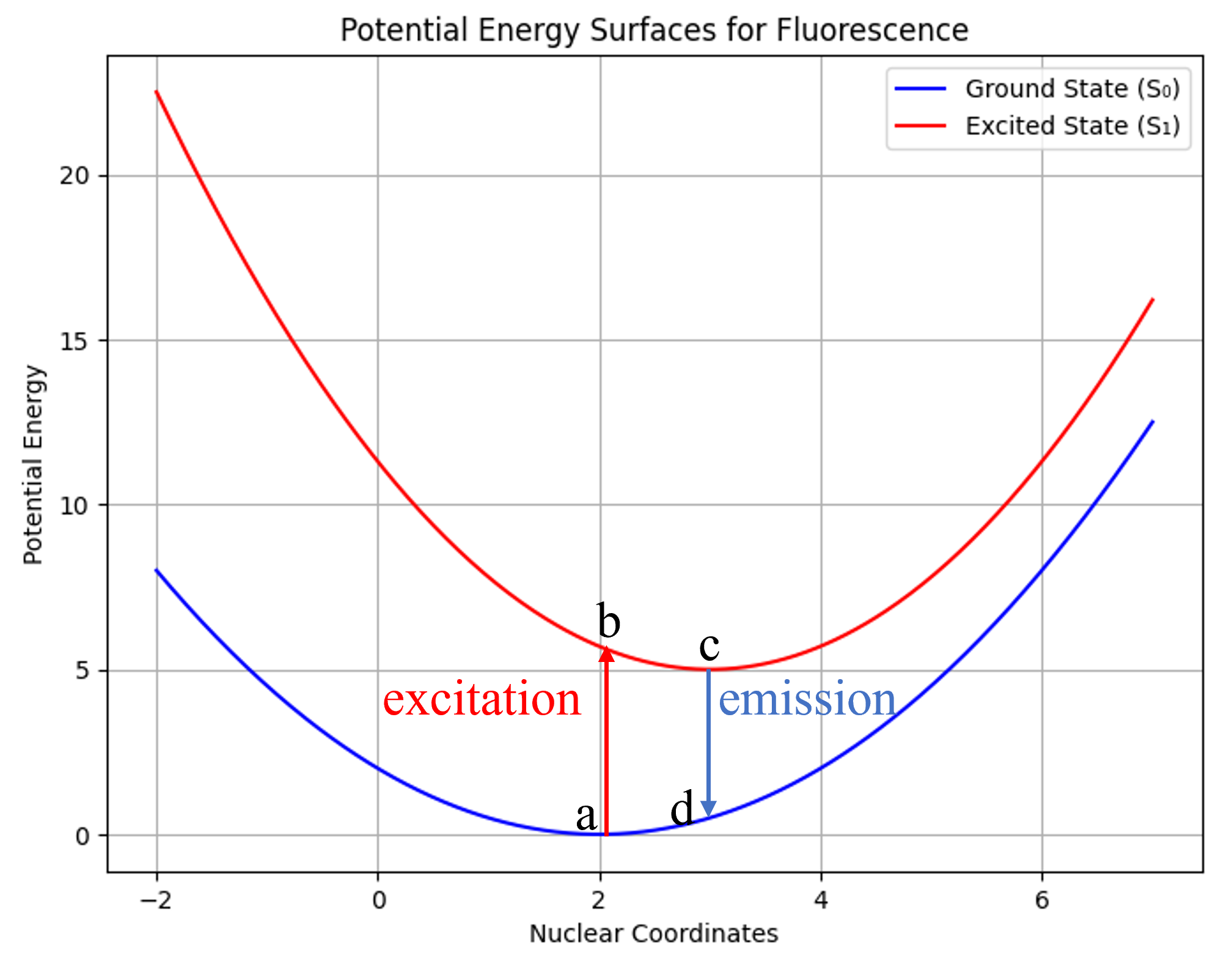
\[E_i(Q) = \frac{1}{2}kQ^2 \tag{1.1}\] \[E_j(Q) = \frac{1}{2}k(Q-Q_0)^2 + \Delta G^0 \tag{1.2}\]同时，我们假设分子总是处于势能面极小点结构，且只考虑第一激发态，则跃迁过程可以简单表示为下图的a → b → c → d：
Fig. n. 简化的荧光过程
假设分子的S0平衡结构为a点，分子在a点处吸收光子跃迁，可以到S1激发态势能面上的b点。由于电子跃迁发生的时间尺度远短于核振动周期的时间尺度，在Born-Oppenheimer近似下，可以认为电子跃迁是瞬时发生的，a点与b点的几何结构一致，这称为Franck-Condon原理。又因为a点与b点的几何结构一致，该模型被称为垂直激发模型，跃迁时的核构型点被称为Franck-Condon点。
FC点通常不是S1势能面上的极小点，即在S1态下，S0极小点的几何结构并不稳定。因此，分子将自发调整结构，从FC点沿某些反应坐标向S1势能面极小点c滑落，这对应Jablonski图中的振动弛豫。在S1平衡结构，分子可以发生辐射跃迁，释放出一个光子并跃迁回S0态的d点。类似地，d点不是S0的极小点，将沿势能面滑落回到S0极小点a。这样，就完成了一整个荧光过程。
接下来，我们借助这个简化的模型将电子从辐射跃迁中分离出来，研究电子对辐射跃迁的影响。
2 辐射跃迁的强度
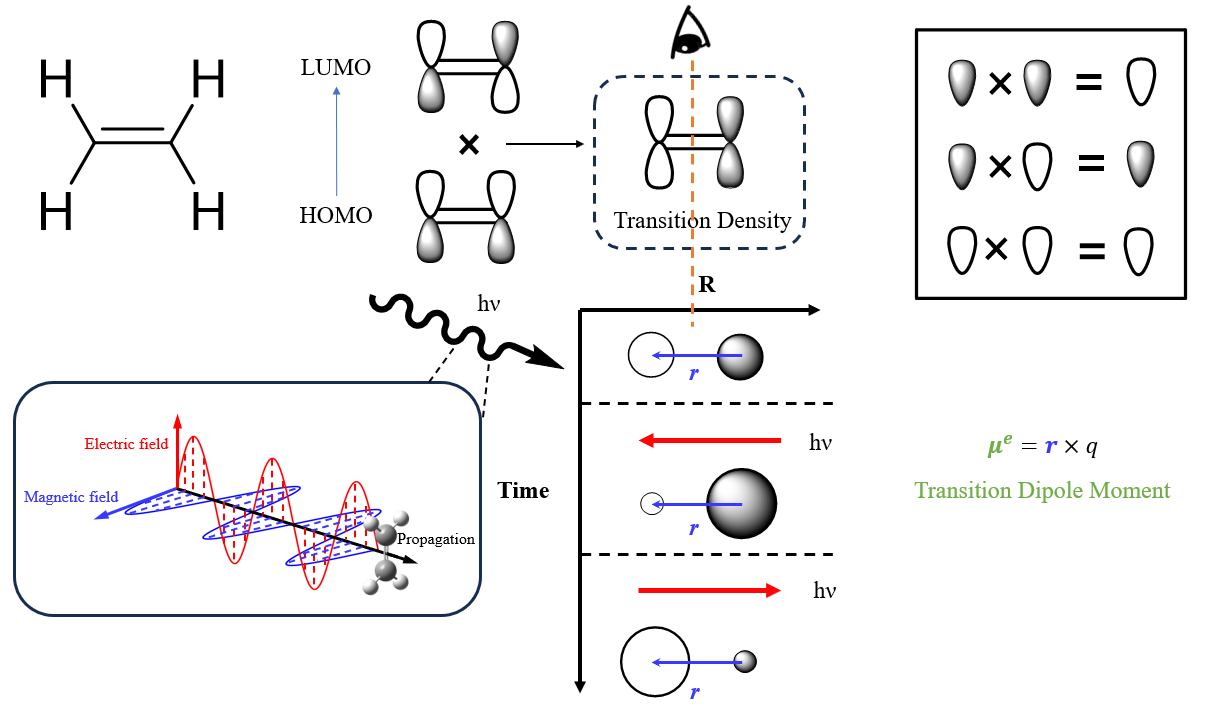
我们在第一节提到过，电子态决定于不同的电子结构。可想而知，当体系从S0态跃迁至S1态时，电子分布会产生改变。我们可以用跃迁密度(Transition Density, TD)来描述这种改变，其定义为：
\[\rho_{ij}(r) = \psi_{i}(r) \times \psi_{j}(r)\]其中：
- $\rho_{ij}(r)$是跃迁密度
- $\psi_{i}(r)$和$\psi_{j}(r)$是初态与末态电子波函数。
我们用一个简单的体系来解释跃迁密度如何影响跃迁。以乙烯为例，它的$\rho_{ij}(r)$是：
\[\rho_{ij}(r) = \psi_{i}(r_1,r_2,r_3....,r_n) \times \psi_{j}(r_1,r_2,r_3....,r_n)\]我们知道，乙烯第一激发态的跃迁是典型的$π-π^*$跃迁，只有HOMO与LUMO参与，所以在单电子近似下，我们可以把上式近似化简为：
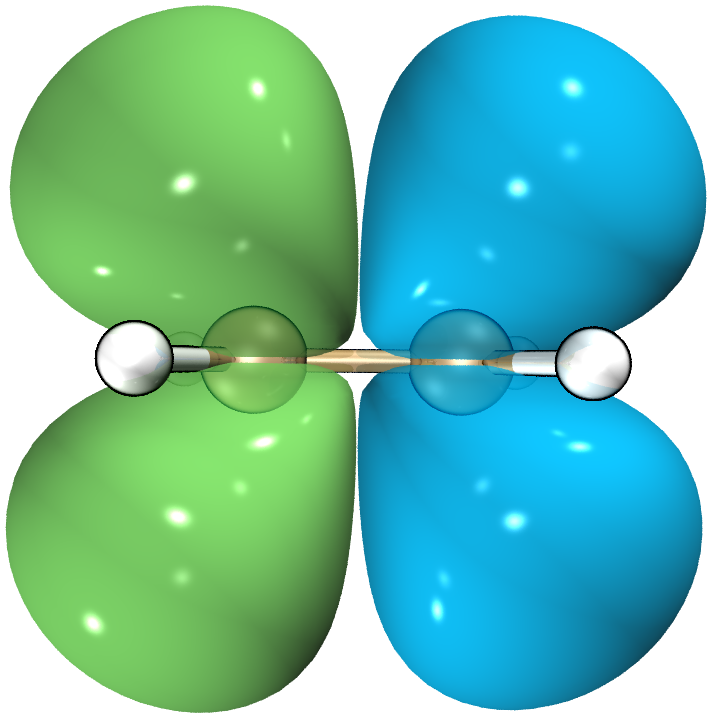
\[\rho_{if}(r) \approx \phi_{HOMO}(r) \times \phi_{LUMO}(r)\]这个式子不够直观，我们可以绘制一个示意图来展现跃迁密度： 
从跃迁密度图中我们可以看到，乙烯的H→L跃迁形成了一个从左→右的跃迁偶极。当电磁辐射穿过乙烯分子时，由于电场的震荡，其电子会随着电场方向改变而产生共振，从而吸收电磁辐射的能量完成跃迁。
不难发现，乙烯吸收电磁辐射的能力与其跃迁偶极的正负电荷中心的距离有关，若跃迁距离长，则吸收截面大，可以更高效地吸收电磁辐射。为了衡量分子吸收电磁辐射的能力，我们引入跃迁偶极矩(Transition Dipole Moment, TDM)来描述电子密度变化与电磁辐射的相互作用能力：
\[\mu_{ij}^e = |\langle \psi_i|\hat{\mu^e}|\psi_j \rangle|^2 \tag{2.1}\]其中：
- $\mu_{ij}^e$是跃迁电偶极矩；
- $\psi_i$、$\psi_j$是初态与末态的电子波函数；
- $\hat{\mu^e}$ 是电偶极矩算符，可以写为：$\hat{\mu^e} = -e\sum_j \mathbf{r}_j$。
除跃迁电偶极矩外，还有跃迁磁偶极矩、跃迁电四极矩等，但通常来说在跃迁电偶极矩未被禁阻时，它们的效应基本可以忽略，因此我们这里只讨论跃迁电偶极矩，我们通常说的跃迁偶极矩指的也就是跃迁电偶极矩。跃迁偶极矩越大，意味着分子与电磁辐射耦合越强，辐射跃迁强度也就越强。事实上，辐射跃迁强度是正比于跃迁偶极矩的模平方的：
\[I_{i \leftarrow j} \propto |\mu_{ij}^e|^2\]现在我们来研究一个稍微复杂一些的模型：
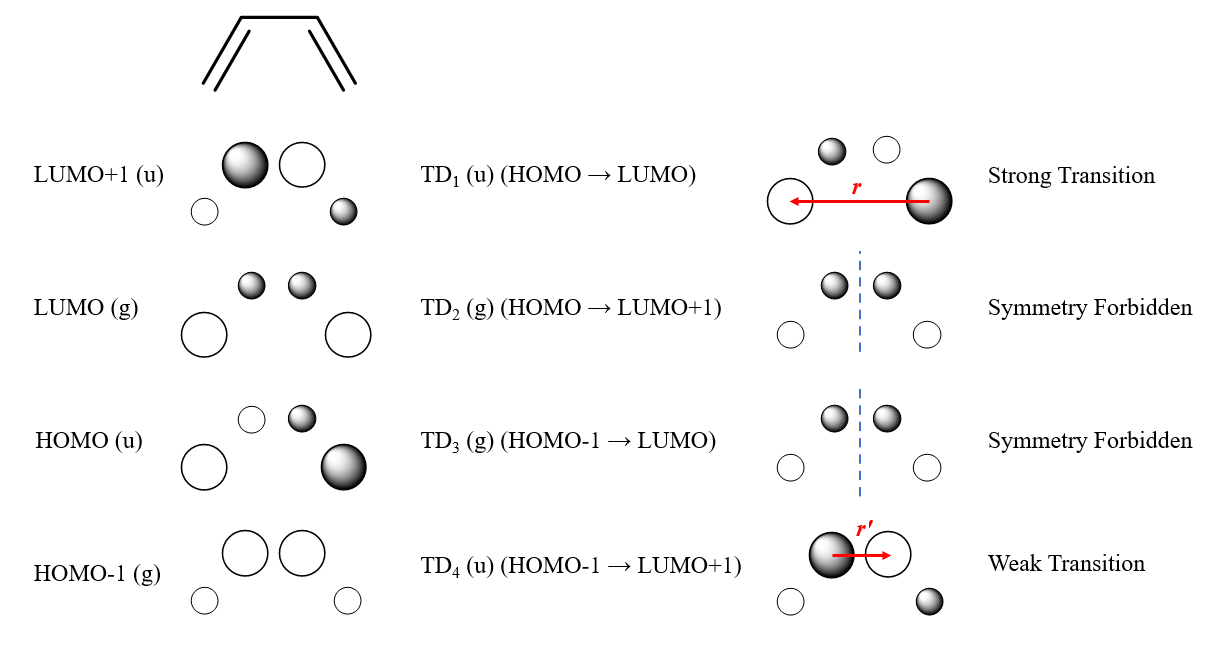
1,3-丁二烯的前线轨道如左侧所示，为绘图方便只绘制了俯视图。我们考虑第一激发态，跃迁轨道对为HOMO→LUMO，其跃迁密度展现了一个较大的跃迁偶极矩，因此，1，3-丁二烯的S1吸收较强。
而HOMO-1→LUMO和HOMO→LUMO+1这两个跃迁的跃迁密度在x方向上是个偶函数，对电场的响应是对称的，$\mu_{ijx}^e$严格为0，不能很好地与电磁波共振，这就构成了对称性禁阻跃迁。可想而知，这两个跃迁吸收电磁辐射的能力很差。
再来看HOMO-1→LUMO+1的跃迁。由于r’小于r，其跃迁偶极矩相较于第一激发态的会小一些，对光子的吸收能力稍弱。然而，这里我们还需要额外关注一件事情：这两个轨道之间的能量差很大，因此，对应激发态的激发能通常也会较大，这意味着该跃迁所吸收的电磁辐射震荡频率很高，而高频振荡的电场传递能量的效率显然比低频振荡的高。我们引入振子强度(oscillator strength)来综合描述辐射跃迁概率，它的数学表示是：
\[f_{ij} = \frac{2m_e\nu}{3\hbar e^2} |\langle \psi_i|\hat{\mu^e}|\psi_j \rangle|^2 \tag{2.2}\]式中：
- $\nu$ 是电磁辐射频率，可以用能量表示：$\nu = \frac{E}{h}$，$E$是以波数(cm⁻¹)为单位的能量。
振子强度可以理解为等效谐振子数量，即如果用简谐振动的电子来模拟实际的跃迁过程，需要多少个这样的经典振子才能产生相同的吸收或发射强度。有了振子强度，再综合辐射场的能量密度，我们就可以计算辐射跃迁的速率。幸运的是，对应公式已经由爱因斯坦帮我们研究出来了：
\[A_{ji} = \frac{8\pi^2e^2\nu^2}{m_ec^3}f_{ij} \tag{2.3}\]式中：
- $e$ 是元电荷；$m_e$ 是电子质量；$c$ 是光速；
代入所有常数，原公式可近似简化为：
\[A_{ji} \approx \frac{3}{2}f_{ij}E^2 \tag{2.4}\]我们可以发现，最终的辐射跃迁速率与振子强度成正比关系，进而也与跃迁偶极矩成正比关系；而由于辐射场的能量密度引入了能量的平方，辐射跃迁速率最终与能量的三次方成正比关系(振子强度里有一个频率也可以转换成能量)，这解释了紫外吸收光谱中，为什么高频区会有很强的吸收峰。
以上，我们借助一个简化的模型描述了电子对辐射跃迁的贡献。由于电子是直接参与跃迁的，其对跃迁的可能性起到决定性作用。接下来，我们将逐步在简化模型中引入原子核的贡献，探讨原子核对跃迁的影响。
3 振动能级
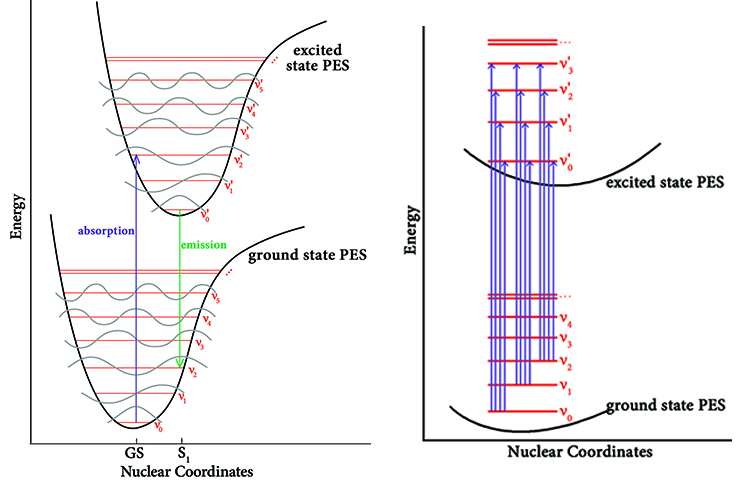
我们在第一节中假设分子总是处于势能面极小点结构来理解垂直激发，而在实际过程中这个假设并不成立。事实上由于不确定性原理，原子不能同时具有精确的位置和动量，分子总是在不断振动的。因此，在某一时刻下，一个宏观体系中必然含有处于不同振动态的分子。在谐振模型下，振动态的能量是离散的，形成了不同的振动能级。将振动能级绘制在势能面上，可得到下图：
Exploring Chemistry With Electronic Structure Methods 3
图中，ν0、ν1、ν2…，ν0‘、ν1‘、ν2‘…指基态与激发态的各振动能级。不同振动相位的分子在垂直激发时，会落到激发态的不同振动能级上，因此吸收的光子能量也不完全相同，这是光谱精细结构(如肩峰)产生的原因:
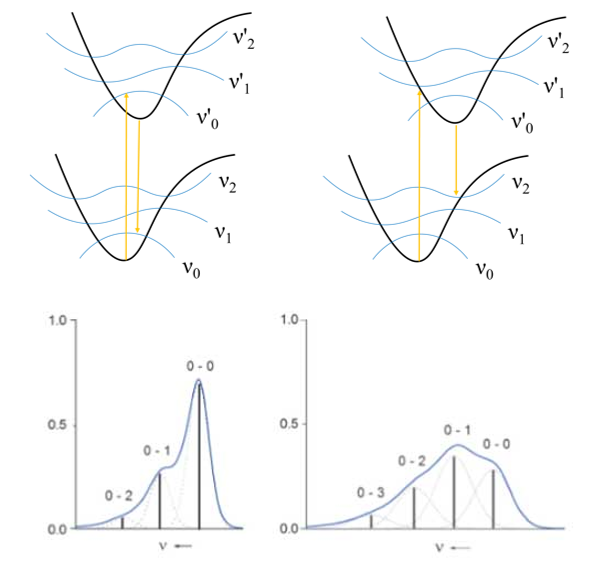Fig. n. 光谱形状的产生原因 Chem. Eur. J. 2012, 18, 8140 – 8149
原文绘制的振动分辨光谱示意图只考虑了从振动基态出发的情况，事实上当体系不处于0K时，还会存在处于振动激发态的分子，其布居数服从Boltzmann分布。这时，1-0、1-1、2-0等从振动激发态起始的跃迁同样可能对光谱形状产生不可忽略的影响。我们可以引入Franck-Condon因子来描述不同振动能级之间跃迁的概率：
\[F_{ij} = |\langle \chi_i|\chi_j \rangle|^2\]对于多维情况，FC因子是各个振动模式的乘积：
\[|\langle \chi_i|\chi_j \rangle|^2 = \prod_k |\langle \chi_{i,k}|\chi_{j,k} \rangle|^2\]式中：
- $F_{ij}$是态$i$与态$j$之间的Franck-Condon因子
- $\langle \chi_i |\chi_j \rangle$表示态$i$与态$j$核波函数的重叠积分
FC因子可以描述振动跃迁的强度，影响其大小的因素主要是两个态之间的能量差。当两个态的能量差较小时，它们的波函数在空间上的分布会更相似，波函数越相似，空间重叠积分就越大，FC因子也越大。
FC因子与跃迁偶极矩共同决定了跃迁强度的大小，考虑FC因子修正后，计算得出的光谱峰形常常可以与实验值进行比较，来指认振动峰的本质。现在，我们可以把跃迁强度的表达式更新为核项与电子项的乘积形式：
\[I_{i \leftarrow j} \propto |\langle \Psi_i|\mu|\Psi_j \rangle|^2 = |\mu_{ij}^e|^2 · F_{ij} ^2\]4 Herzberg-Teller效应
前述垂直激发过程可以正确描述多数跃迁过程，但有少数情况例外。以苯为例，苯分子具有$D_{6h}$高阶点群对称性，它的激发由于跃迁偶极矩的相互抵消，会导致FC项精确为0，跃迁受到对称性禁阻。然而，实际上可以观察到苯分子的激发，因为真正的激发过程并非像Franck-Condon原理描述的一样是完全垂直的。
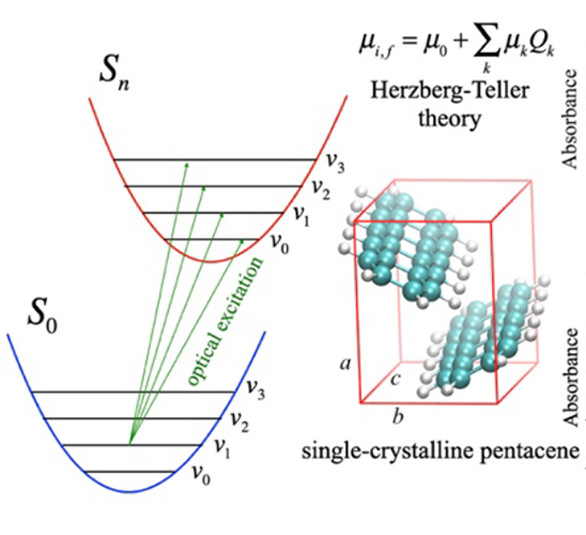Fig. n Herzberg-Teller效应 J. Phys. Chem. A 2020, 124, 44, 9156–9165
由于核运动事实上会扰动电子态，导致电子波函数在扰动下不再是严格的绝热近似下的本征态，这使得某些在绝热近似下禁阻的跃迁可以变为允许。我们引入Herzberg-Teller效应来描述这种扰动，考虑电子跃迁偶极矩对核坐标的依赖性。在平衡构型附近，电子跃迁偶极矩可以对核坐标进行泰勒展开：
\[\mu_{ij}^e = \mu_{ij}^0 + \sum_k (\frac{\partial \mu_{ij}}{\partial Q_k})_0 Q_k + \frac{1}{2}\sum_{k,l} (\frac{\partial^2 \mu_{ij}}{\partial Q_k \partial Q_l})_0 Q_k Q_l + ...\]式中：
- $\mu_{ij}^e$ 是电子跃迁偶极矩
- $\mu_{ij}^0$ 是平衡构型下的跃迁偶极矩，$Q_k$ 是第k个简正坐标
- $(\frac{\partial \mu_{ij}}{\partial Q_k})_0$ 是跃迁偶极矩对简正坐标的一阶导数
通常Herzberg-Teller高阶项贡献相对较小，在小振幅的情况下很少考虑二阶项或更高的项。考虑一阶Herzberg-Teller效应的跃迁强度可以表示为：
\[I_{i \leftarrow j} \propto |\langle \Psi_i|\mu|\Psi_j \rangle|^2 = |\mu_{ij}^0\langle \chi_i|\chi_j \rangle + \sum_k (\frac{\partial \mu_{ij}}{\partial Q_k})_0 \langle \chi_i|Q_k|\chi_j \rangle|^2 \tag{4.1}\]式中：
- $\mu_{ij}^0\langle \chi_i |\chi_j \rangle$是Franck-Condon项，对应于零阶近似
- $\sum_k (\frac{\partial \mu_{ij}}{\partial Q_k})_0 \langle \chi_i |Q_k |\chi_j \rangle$是Herzberg-Teller一阶校正项，包含了电子-振动耦合效应
当$\mu_{ij}^0 = 0$时（即跃迁在FC近似下被禁阻），Herzberg-Teller项可能会成为跃迁的主要贡献，例如：
- 跃迁过程会受到受到宇称选择规则的限制。电偶极跃迁算符的宇称是奇宇称，只能发生在初态和末态的宇称不同的情况下，否则该跃迁是禁阻的。如苯分子的 $A_{1g} \rightarrow B_{2u}$ 跃迁。
- 跃迁过程会受到对称性选择定则的限制。两个跃迁轨道不可约表示$\Gamma_A$和$\Gamma_B$的直积需要包含完全对称的表示，否则该跃迁是禁阻的。如苯分子的$B_{2u} \rightarrow B_{1u}$ 跃迁。
- 跃迁要求两个轨道存在重叠，否则不能产生非零的跃迁偶极矩，如如羰基孤对电子的$n \rightarrow \pi^*$跃迁是禁阻/弱允许的。
- 跃迁过程的自旋角动量变化是受自旋选择定则限制的。在电偶极跃迁中，要求$\Delta S = 0$，即自旋角动量不能变化，否则跃迁是禁阻的。如蒽的系间窜越过程。如果把HT的哈密顿微扰项算进来，就产生了旋轨耦合打破禁阻。
这个禁阻不在HT效应的影响范围内：
- 根据角动量耦合的守恒定律，跃迁过程的轨道角动量变化是受限的。对于电偶极跃迁，由于光子携带1的角动量，要求$\Delta \lambda = \pm 1$，否则该跃迁是禁阻的。如氢原子$1s \rightarrow 2s$的跃迁。
5 非辐射跃迁
荧光领域有一条很著名的规则——卡莎规则(kasha’s rule)，它指出分子在光激发后，无论最初被激发到哪个高能态（如$S_2$、$S_3$等），最终的发光（荧光或磷光）通常仅来源于最低激发态（如$S_1$或$T_1$。卡莎规则是一条经验规则，尽管后来发现了一些反卡莎发射的分子，但总体来看，大部分有机分子的荧光发射还是遵循卡莎规则的。要了解卡莎规则背后的物理学原理，就要解释清楚除辐射跃迁以外的另一种无光子参与跃迁形式。
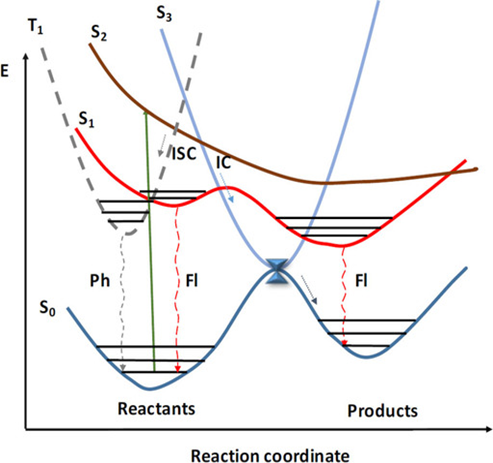Fig. n. 势能面上的荧光过程 Chem. Asian J. 2019, 14, 700.
在上图中，我们看到从激发态回到基态的通道还包括一类不发射光子的跃迁过程(IC, ISC)，这类跃迁被称为非辐射跃迁，特征是体系会通过非光子途径将激发态的能量耗散到周围环境中，到达另一个态。非辐射跃迁速率可以用费米黄金定则(Fermi’s Golden Rule)来计算：
设初态为 $\psi_i$，末态为 $\psi_j$，对应能量为 $E_i$ 和 $E_j$，则：
\[k_{\text{nr}} = \frac{2\pi}{\hbar} \bigl|\langle \psi_i | \hat{H} | \psi_j \rangle \bigr|^2 \rho(E_j) \tag{5.0.1}\]式中：
$\hat{H}$ 是两个态之间耦合的哈密顿量算符，可以是非绝热耦合(IC)、旋轨耦合(SOC)、振动耦合等。$\langle \psi_i | \hat{H} | \psi_j \rangle$包含了核项与电子项：
\[\langle \psi_i | \hat{H} | \psi_j \rangle = \langle \chi_i|\chi_j \rangle \langle \psi_i|\frac{\partial}{\partial Q_\alpha}|\psi_j \rangle\]其中，$\langle \chi_i | \chi_j \rangle$是FC因子，我们在第3节已经介绍过，它与两个态之间的能量差相关。两个态之间的能量差越小，FC因子就越大，有利于非辐射跃迁。由此可知：能量差越小，$k_{\text{nr}}$通常越大。
能隙定律(energy gap law)：内转换的速率随参与跃迁的两个电子态的能隙间隔呈指数下降。根据能隙定律，可推知两个激发态之间的能量差越低，内转换速率就越快。通常高激发态间的能量差比较小(相对于S0-S1来说)，因此内转换速率必然远远大于辐射速率，这也是卡莎规则的由来。
$\rho(E_j)$为态密度，表示在单位能量间隔内可找到的末态数目。态密度受两个态之间能量匹配的影响，在能量近似匹配的位置，对应的振动态密度往往较大，从而使跃迁速率增大，其数学表示为： \(\rho(E_j) = \frac{1}{Z}\int \exp(-\frac{E_j(Q)}{k_BT})dQ\)
由于$\rho(E_j)$表达式包含了一个对核坐标的积分，不能直观地进行比较，我们需要对该公式进行一些推导。经过一些笔者看不太懂的炫酷数学变换后，态密度这一项被展开，Golden Rule转换成了这样的形式：
\[k_{n r} = \frac{2\pi}{\hbar} \frac{|V_{i j}|^2}{\sqrt{4\pi \lambda k_B T}} \exp\left(-\frac{(\Delta G + \lambda)^2}{4\lambda k_B T}\right) \tag{5.0.2}\]其中：
- $V_{ij}$ 表示电子转移的电子态耦合强度，由$H_{ij}$拆出FC因子而来，而后者似乎是在积分时给积掉了。
- $\Delta G$ 表示电子转移的吉布斯自由能差。
- $\lambda$ 表示重组能，反映了核构型和溶剂对电子转移过程的阻碍作用。
$5.0.2$ 式是Marcus在1956年提出的电子转移理论中Marcus速率公式的一种形式。该理论原先是研究有机化学中受体与给体之间的电子转移的，光化学借用过来效果也不错。
从Marcus公式中可以看到，影响$k_{nr}$的因素有三个，我们来分析一下它们的影响。
- $\lambda$是阻碍电子转移的，它的值是正值。我们先撇开指数项(因为指数项有$\Delta G$参与)，单看$\frac{1}{\sqrt{4\pi \lambda k_B T}}$这一项，可以发现重组能增加对非辐射跃迁是不利的。
在指数项$\exp\left(-\frac{(\Delta G + \lambda)^2}{4\lambda k_B T}\right)$中，$(\Delta G + \lambda)^2$这部分十分引人注目。可以发现，由于$\Delta G$为负值，$\lambda$为正值，这一项越接近0，$k_{nr}$越大，即$\Delta G$与$\lambda$越接近，对非辐射跃迁越有利。根据指数项的特点，Marcus速率公式预测了Marcus反转区，即当热力学驱动力增加到一定程度时，电子转移速率反而会降低。
- $V_{ij}$毫无疑问与$k_{nr}$成正比关系，即两个电子态之间的耦合越大，$k_{nr}$越大。$V_{ij}$是否为0决定了非辐射跃迁是否可以发生，常见的通道包括内转换和系间窜越。
5.1 内转换(Internal Conversion, IC)
内转换指同多重度（如同为单重态）的电子激发态之间的无辐射过程。在绝热近似下，两个电子态的波函数随核坐标变化彼此独立，没有有效的转化通道。而当绝热近似被破坏，两个电子态在核坐标空间产生一定的关联时，就可以通过内转换转移能量。
我们引入非绝热耦合（Non-adiabatic Coupling，NAC）来描述这种关联。设 $|\Phi_i(\mathbf{r};\mathbf{R})\rangle$ 是在给定核坐标 $\mathbf{R}$ 下的第 $i$ 个电子本征态，则非绝热耦合一般定义为两个电子态 $|\Phi_i\rangle$ 和 $|\Phi_j\rangle$ 间的导数内积：
\[d_{ij}(\mathbf{R}) = \langle \Phi_i(\mathbf{r};\mathbf{R}) \mid \nabla_{\mathbf{R}} \mid \Phi_j(\mathbf{r};\mathbf{R}) \rangle \tag{5.1.1}\]式中：$\nabla_{\mathbf{R}}$ 表示对核坐标 $\mathbf{R}$ 的梯度算符。
非绝热耦合量体现了当核坐标发生变化时，电子态之间的混合与转化程度。当该项不为0时，态$i$与态$j$就可以通过内转换进行无辐射转换。该过程通常伴随振动弛豫，使多余的电子能量转化为分子内振动势能。
NAC的分布情况与圆锥交叉有关，见5.3节。
5.2 系间窜跃(Intersystem Crossing, ISC)
系间窜跃指激发态从一种自旋多重度跃迁至另一种自旋多重度的无辐射过程，例如从单重态 $S_1$ 转移至三重态 $T_1$。由于自旋角动量发生了改变，这一过程受到自选选择定则严格禁阻，在理想情况下不能发生。然而实际上由于电子自旋与轨道运动会相互耦合，电子态并不一定是严格纯态，使得系间窜越过程可能实现。我们引入自旋-轨道耦合（Spin-Orbit Coupling, SOC）来描述这种耦合效应：
\[\hat{H}_{\mathrm{SO}} = \xi(r)\mathbf{L}\cdot\mathbf{S} \tag{5.2.1}\]式中：
- $\mathbf{L}$是电子的轨道角动量算符；$\mathbf{S}$是电子的自旋角动量算符。
- $\xi(r)$是自旋-轨道耦合参数，它的数学表示是： \(\xi(r) = \frac{\alpha^2}{2m_e^2 c^2} \frac{1}{r}\frac{dV(r)}{dr} \tag{5.2.2}\) 式中：
- $\alpha$ 是精细结构常数（$\alpha \approx 1/137$）；$m_e$ 是电子质量；$c$ 是光速；
- $V(r)$ 是作用于电子上的球对称位势（如原子核场势）；
根据$\hat{H}_{\mathrm{SO}}$的数学表示，可以推知一些能够影响系间窜越的因素：
- 几何结构畸变可能会导致轨道分子轨道能级重新分布、能隙变化，以及轨道成分（如p、d轨道混合比例）和对称性的改变，进而影响轨道角动量特性，改变$\mathbf{L}\cdot\mathbf{S}$项，从而导致单重态与三重态之间产生耦合；
- 强电荷转移、外加电场或磁场的存在可以改变外势项$\frac{1}{r}\frac{dV(r)}{dr}$，导致单重态与三重态之间产生耦合。而一些重原子(如Br、I、Se等)的核电荷数很高，其原子核的库仑势场可以起到类似外加电场的效应，这称为重原子效应；
- 一些轨道角动量改变的禁阻跃迁(如羰基氧孤对电子的$n- \pi^*$跃迁)往往有比较强的旋轨耦合，因为轨道角动量的变化可以补偿自旋角动量的变化。
El Sayed rule: 由于系间窜越时有电子自旋翻转发生，为补偿电子自旋翻转所导致的动量改变，必需有一个电子在相互垂直的轨道上跳跃来平衡这种动量改变，这时系间窜越才容易发生。
5.3 势能面交叉
虽然势能面交叉与内转换、系间窜越等非辐射途径并不是并列关系，但跟非辐射跃迁是密切相关的。想了很久，最后还是把势能面交叉放在这里了。
势能面交叉是指两个电子态对应的势能面在某些核构型点相互接近、相交或接近简并的现象。在Born-Oppenheimer近似下，不同电子态的势能面是相互独立的，分子通常沿着单个势能面运动；但是在势能面相交或近似相交区域，Born-Oppenheimer近似将失效，电子和核坐标强烈耦合，分子有较高概率发生电子态之间的无辐射跃迁。这种区域往往是非绝热过程的关键所在。
根据两个电子态的自旋多重度，势能面交叉点可以分为两种情况：
最小能量交叉点（MECP, Minimum Energy Crossing Point）
形成MECP的两个态能量简并，但自旋多重度不同，两个态不简并。在该点附近两态的能量几乎相同，自旋态混合效率增强，体系有更高概率实现系间窜越。
在MECP结构下，体系的振动导致的瞬时旋轨耦合往往也能促使体系发生系间窜越。因此除了旋轨耦合，能量匹配也是影响ISC速率的重要因素。
最小能量圆锥交叉点（MECI, Minimum Energy Conical Intersection）
形成MECI的两个态能量简并，自旋多重度相同，形成简并态。因交叉点通常形成类似圆锥形状的拓扑结构，得名圆锥交叉（Conical Intersection, CI）。其实CI还分为圆锥交叉和圆锥避免交叉两种情况，就不展开叙述了。
两个态能量相差越大，简并特征越微弱，电子态之间的往往相互独立；越接近CI点，电子态之间的界限越模糊，NAC越大；在CI点附近，由于电子态简并，5.1.1式中$\nabla_{\mathbf{R}}$对波函数的影响不再是平滑渐进的，会随核坐标剧烈变化，因此态间的非绝热耦合会急剧增强，往往会发生迅速的内转换。因此CI点是NAC强度的“热点”。
6 量子产率
在研究光物理过程时，我们通常将辐射过程与非辐射过程统一纳入一个速率方程中描述。如果我们以 $k_r$ 表示辐射跃迁速率，以 $k_{nr}$ 表示所有非辐射通道的总速率，那么激发态总衰减速率为：
\[k_{\text{tot}} = k_{r} + k_{nr}\]量子产率(Quantum Yield)为发光光子数与吸收光子数的比例，可写作：
\[\Phi = \frac{k_r}{k_{r} + k_{nr}}\]由该公式可知，辐射跃迁与非辐射跃迁是竞争关系。当非辐射过程占主导时（$k_{nr} \gg k_r$），系统的量子产率将接近零，发光强度显著降低。
荧光寿命是$\frac{1}{k_{r} + k_{nr}}$。